题目内容
已知函数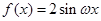 ·
·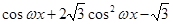 (其中
(其中 >o),且函数
>o),且函数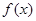 的最小正周期为
的最小正周期为
(I)求f(x)的最大值及相应x的取值
(Ⅱ)将函数y= f(x)的图象向左平移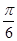 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
(1)f(x)的最大值为2,对应x的取值是x=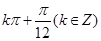
(2)函数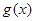 的增区间为[
的增区间为[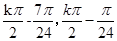 ]
] 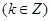 ;减区间为[
;减区间为[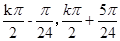 ],
],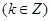 .
.
解析试题分析:解:(Ⅰ)因为 , 2分
, 2分
因为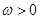 ,函数
,函数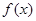 周期为
周期为 ,所以
,所以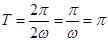 ,
,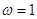 4分
4分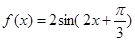 , f(x)的最大值为2,对应x的取值是x=
, f(x)的最大值为2,对应x的取值是x=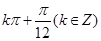 6分
6分
(Ⅱ)由(Ⅰ)知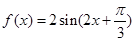 . 将函数
. 将函数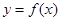 的图象向左平移
的图象向左平移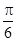 个单位后得到函数
个单位后得到函数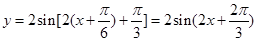 的图象,再将所得图象各点的横坐标缩小为原来的
的图象,再将所得图象各点的横坐标缩小为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数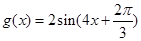 . 9分
. 9分
由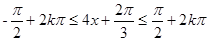 ,
,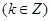 ;得
;得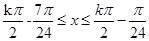
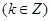
由
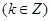 ;得
;得
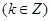
故函数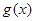 的增区间为[
的增区间为[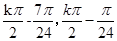 ]
] 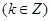 ;
;
减区间为[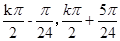 ],
],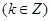 ..13分
..13分
考点:三角函数的化简和性质
点评:主要是考查了三角函数的性质以及二倍角公式的运用,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
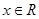 ,
,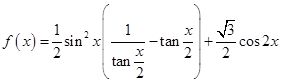 .
.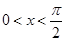 ,求
,求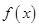 的单调的递减区间;
的单调的递减区间;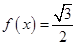 ,求
,求 的值.
的值. .
.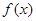 的最小值和最小正周期;
的最小值和最小正周期;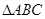 内角
内角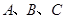 的对边分别为
的对边分别为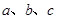 ,且
,且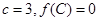 ,
,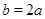 ,求
,求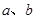 的值.
的值.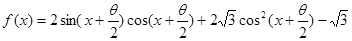
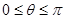 ,求
,求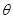 使函数
使函数 为偶函数。
为偶函数。 ∈[-π,π]的
∈[-π,π]的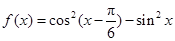 .
.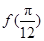 的值;
的值; 在
在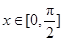 的最大值.
的最大值.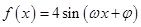 ,
,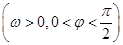 ,
,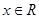 的最小正周期是
的最小正周期是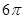 ,其图象经过点
,其图象经过点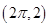 .
.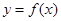 的表达式;
的表达式;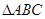 的三个内角分别为
的三个内角分别为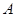 ,
,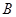 ,
,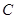 ,若
,若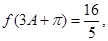
 ;求
;求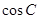 的值.
的值.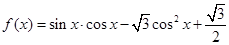 .
. 的对称轴方程和单调递增区间;
的对称轴方程和单调递增区间;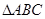 中,
中,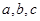 分别是角
分别是角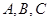 的对边,且
的对边,且 ,
,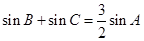 ,求
,求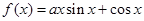 ,且
,且 在
在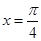 处的切线斜率为
处的切线斜率为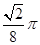 .
. 的值,并讨论
的值,并讨论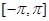 上的单调性;
上的单调性;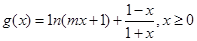 ,其中
,其中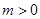 ,若对任意的
,若对任意的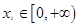 总存在
总存在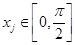 ,使得
,使得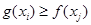 成立,求
成立,求 的取值范围.
的取值范围.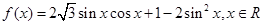 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;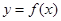 的图像上各点的纵坐标保持不变,横坐标缩短到原来的
的图像上各点的纵坐标保持不变,横坐标缩短到原来的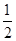 ,把所得到的图像再向左平移
,把所得到的图像再向左平移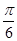 单位,得到的函数
单位,得到的函数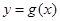 的图像,求函数
的图像,求函数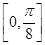 上的最小值.
上的最小值.