题目内容
11.已知集合A={x|x2-2x-3=0},集合B={-1,0,1,2,3},且集合M满足A⊆M⊆B,则M的个数为( )| A. | 32 | B. | 16 | C. | 8 | D. | 7 |
分析 先求出集合A={-1,3},根据A⊆M⊆B便知M中一定含有元素-1,3,而0,1,2可能为集合M的元素,从而便可得到M的个数为${{C}_{3}}^{0}+{{C}_{3}}^{1}+{{C}_{3}}^{2}+{{C}_{3}}^{3}$,这样便可得出M的个数.
解答 解:A={-1,3},A⊆M;
∴-1∈M,3∈M;
又M⊆B;
∴0,1,2,可能是M的元素;
∴M的个数为:${{C}_{3}}^{0}+{{C}_{3}}^{1}+{{C}_{3}}^{2}+{{C}_{3}}^{3}={2}^{3}=8$.
故选:C.
点评 考查一元二次方程的解法,列举法、描述法表示集合,子集的概念,组合数的概念,以及二项式定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知ab>0,bc<0,则直线ax+by+c=0通过( )
| A. | 第一、二、四象限 | B. | 第一、二、三象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |
16.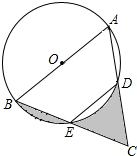 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
1.设i是虚数单位,则-1+i-i2+i3-i4+…-i20=( )
| A. | 1 | B. | 0 | C. | -1 | D. | i |