题目内容
18.梯形ABCD中,AB∥CD,直线AB、BC、CD、DA分别与平面α交于点E、G、F、H,那么一定有G∈直线EF,H∈直线EF.分析 由已知得E、G、F、H都在平面ABCD上,且E、G、F、H都在平面α上,由公理三,得平面ABCD∩α=EF,由此能求出答案.
解答  解:∵梯形ABCD中,AB∥CD,直线AB、BC、CD、DA分别与平面α交于点E、G、F、H,
解:∵梯形ABCD中,AB∥CD,直线AB、BC、CD、DA分别与平面α交于点E、G、F、H,
∴E、G、F、H都在平面ABCD上,
且E、G、F、H都平面α,
∴由公理三,得平面ABCD∩α=EF,
∵G和H都是平面ABCD与平面α的公共点,
∴G∈直线EF,E∈直线EF.
故答案为:∈,∈.
点评 本题考查点与直线的位置关系的判断与证,是基础题.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
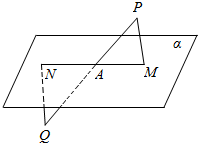 如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.
如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.