题目内容
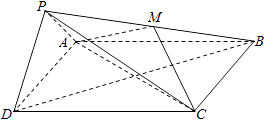
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() ,
,![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
【答案】见解析
【解析】(1)因为![]() ,所以
,所以![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,
的中位线,
又![]() 所以
所以![]() ,所以
,所以![]() ,(2分)
,(2分)
又点![]() 在椭圆上,所以
在椭圆上,所以![]() ①,
①,
又![]() ②,①②联立解得
②,①②联立解得![]() ,
,![]() ,
,
所以所求椭圆的标准方程为![]() .(4分)
.(4分)
(2)因为直线![]() 与圆
与圆![]() 相切,所以
相切,所以![]() ,即
,即![]() ,
,
联立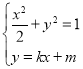 ,消去
,消去![]() ,可得
,可得![]() .(6分)
.(6分)
设![]() ,
,![]() ,因为直线
,因为直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ,故
,故![]() .
.
由根与系数的关系可得![]() ,
,![]() ,
,
所以![]() ,(8分)
,(8分)
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以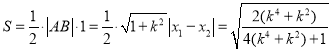 .(10分)
.(10分)
设![]() ,则
,则![]() ,
,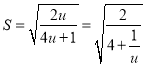 ,
,
显然![]() 关于
关于![]() 的函数在定义域内单调递增,
的函数在定义域内单调递增,
所以![]() ,即
,即![]() .
.
故![]() 的面积
的面积![]() 的取值范围为
的取值范围为![]() .(12分)
.(12分)

练习册系列答案
相关题目