题目内容
【题目】设△ABC的内角A，B，C的对边分别为a，b，c，b=2 
，B= 
．
（1）若a=2，求角C；
（2）若D为AC的中点，BD= 
，求△ABC的面积．
【答案】
（1）解：在△ABC中，由正弦定理可得： 
，
∴sinA= 
= 
= 
，
又a＜b，∴A为锐角，A= 
，
∴C=π﹣A﹣B= ．
（2）解：在△ABC中，由余弦定理可得： 
= 
= 
=﹣ ，化为：a2+c2+ac=12．
在△ABD与△BCD中，由余弦定理可得：cos∠ADB+cos∠BDC= 
+ 
=0，
化为：a2+c2=10．
与a2+c2+ac=12联立解得：ac=2，
∴S△ABC= 
= 
【解析】（1）在△ABC中，由正弦定理可得： ，可得sinA= ，又a＜b，可得A为锐角，可得C=π﹣A﹣B．（2）在△ABC中，由余弦定理可得： = =﹣ ，化为：a2+c2+ac=12．在△ABD与△BCD中，由余弦定理可得：cos∠ADB+cos∠BDC=0，化为：a2+c2=10．联立解出即可得出．
【考点精析】认真审题，首先需要了解正弦定理的定义(正弦定理:
)，还要掌握余弦定理的定义(余弦定理:
;
;
)的相关知识才是答题的关键．
备战中考寒假系列答案
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动，随机对该市18～68岁的人群抽取一个容量为n的样本，并将样本数据分成五组：[18，28），[28，38），[38，48），[48，58），[58，68），再将其按从左到右的顺序分别编号为第1组，第2组，…，第5组，绘制了样本的频率分布直方图；并对回答问题情况进行统计后，结果如下表所示．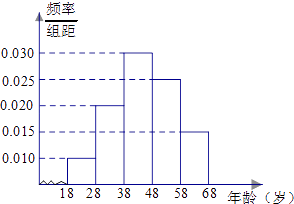 
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18，28） | 5 | 0.5 |
第2组 | [28，38） | 18 | a |
第3组 | [38，48） | 27 | 0.9 |
第4组 | [48，58） | x | 0.36 |
第5组 | [58，68） | 3 | 0.2 |
（1）分别求出a，x的值；
（2）从第2，3，4组回答正确的人中用分层抽样方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，决定在所抽取的6人中随机抽取2人颁发幸运奖，求：所抽取的人中第2组至少有1人获得幸运奖的概率．
