题目内容
【题目】如果对于一切的正实数x、y，不等式 
﹣cos2x≥asinx﹣ 
都成立，则实数a的取值范围
【答案】[﹣3，3]
【解析】解：由于y＞0，则 
+ 
，由于对于一切的正实数x、y，不等式 ﹣cos2x≥asinx﹣ 
都成立，
即 + ≥3≥asinx+cos2x对任意的正实数x都成立，
故sin2x﹣asinx+2≥0对任意的正实数x都成立，
令f（t）=t2﹣at+2，t∈[﹣1，1]
若使f（t）=t2﹣at+2≥0在t∈[﹣1，1]时恒成立，
则必有△=a2﹣8≤0或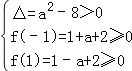 
，
解得﹣2 
≤a≤2 或﹣3 
或2 
a≤3
故使sin2x﹣asinx+2≥0对任意的正实数x都成立的a的范围是[﹣3，3]，
故对于一切的正实数x、y，不等式 ﹣cos2x≥asinx﹣ 都成立，则实数a的取值范围为[﹣3，3]，
所以答案是：[﹣3，3]
【考点精析】认真审题，首先需要了解同角三角函数基本关系的运用(同角三角函数的基本关系：
；
;（3） 倒数关系：
)．
练习册系列答案
相关题目
