题目内容
一个袋子中装有六个大小形状完全相同的小球,其中一个编号为1,两个编号为2,三个编号为3.现从中任取一球,记下编号后放回,再任取一球,则两次取出的球的编号之和等于4的概率是________.

[解析] 列举可知,共有36种情况,和为4的情况有10种,所以所求概率P= =
= .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在某医学实验中,某实验小组为了分析某药物用药量与血液中某种抗体水平的关系,选取六只实验动物进行血检,得到如下资料:
| 动物编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 用药量x(单位) | 1 | 3 | 4 | 5 | 6 | 8 |
| 抗体指标y(单位) | 3.4 | 3.7 | 3.8 | 4.0 | 4.2 | 4.3 |
记s为抗体指标标准差,若抗体指标落在(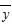 -s,
-s,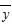 +s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
+s)内,则称该动物为有效动物,否则称为无效动物.研究方案规定先从六只动物中选取两只,用剩下的四只动物的数据求线性回归方程,再对被选取的两只动物数据进行检验.
(1)求选取的两只动物都是有效动物的概率;
(2)若选取的是编号为1和6的两只动物,且利用剩余四只动物的数据求出y关于x的线性回归方程为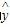 =0.17x+a,试求出a的值;
=0.17x+a,试求出a的值;
(3)若根据回归方程估计出的1号和6号动物抗体指标数据与检验结果误差都不超过抗体指标标准差,则认为得到的线性回归方程是可靠的.试判断(2)中所得线性回归方程是否可靠.
参考公式:样本数据x1,x2,…,xn的标准差:
S=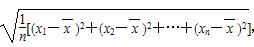 ,其中
,其中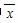 为样本平均数.
为样本平均数.
 (x
(x +x
+x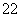 +x
+x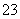 +x
+x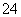 -16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( )
-16),则数据x1+2,x2+2,x3+2,x4+2的平均数为( ) 为整数的概率是________.
为整数的概率是________. B.
B.
 D.
D.
 B.
B.
 D.
D.