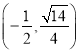Question

【题目】设函数的反函数为，若存在函数使得对函数定义域内的任意都有，则称函数为函数的“Inverse”函数.

（1）判断下列哪个函数是函数的“Inverse”函数并说明理由.

①；②；

（2）设函数存在反函数，证明函数存在唯一的“Inverse”函数的充要条件是函数的值域为；

（3）设函数存在反函数，函数为的一个“Inverse”函数，记，其中，若对函数定义域内的任意都有，求所有满足条件的函数的解析式.

Answer 1

【答案】（1）②是函数f(x)=log2x的“Inverse”函数，理由见解析；（2）证明见解析；（3）.

【解析】

（1）分别判断①和②是否满足即可得到结果；

（2）先证充分性，若函数的值域为，设其定义域为D，则函数的定义域为，值域为D， 令，，判断是否满足，证明其存在性，再设函数和都为函数的“Inverse”函数且不相同，利用反证法证明唯一性；再证必要性，若函数存在唯一的“Inverse”函数，同样利用反证法，假设函数的值域为，令，，通过证明函数和都为函数的“Inverse”函数且不相同，这与唯一性矛盾，从而得证；

（3）由（2）知，是的一个“Inverse”函数，易得，，即，根据一一对应的性质可得，所以.

（1）易得，对于①，，故①不是，

对于②，，故②是函数的“Inverse”函数；

（2）先证充分性，若函数的值域为，设其定义域为D，

则函数的定义域为，值域为D，

令，，

则对任意都有，，

故函数为函数的“Inverse”函数，存在性得证；

设函数和都为函数的“Inverse”函数且不相同，

则存在，，，且，因为的值域为，

故存在，使得，即，，

则，矛盾，故唯一性得证.

所以函数存在唯一的“Inverse”函数.

再证必要性，若函数存在唯一的“Inverse”函数，

即存在唯一的函数满足，下面用反证法证明必要性.

假设函数的值域为，

令，，

则对任意都有，，

且，，

函数和都为函数的“Inverse”函数且不相同，这与唯一性矛盾，

所以函数的值域为，必要性得证.

综上，函数存在唯一的“Inverse”函数的充要条件是函数的值域为；

（3）由（2）知，是的一个“Inverse”函数，

由反函数的性质可知，和都是一一对应的.

则，

又，则，

即，根据一一对应的性质可得，

则，所以满足条件的函数的解析式为.