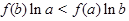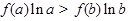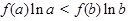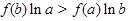题目内容
已知R上的函数y=f(x),其周期为2,且x∈(-1,1]时f(x)=1+x2,函数g(x)=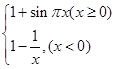 ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| A.11 | B.10 | C.9 | D.8 |
C
解析试题分析:易知,当 时零点分别是,0,1,2,4,5共5个,当
时零点分别是,0,1,2,4,5共5个,当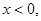 函数在区间
函数在区间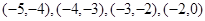 间分别有一个零点,故共9个零点.
间分别有一个零点,故共9个零点.
考点:函数的零点
点评:解决本题的关键是把函数有零点的问题,转化成两函数在某区间内有交点的问题,属中档题.

练习册系列答案
相关题目
函数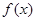 的图象如图所示,下列数值排序正确的是
的图象如图所示,下列数值排序正确的是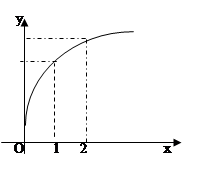
A.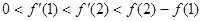 |
B.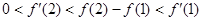 |
C.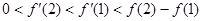 |
D.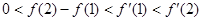 |
已知函数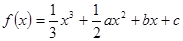 在
在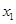 处取得极大值,在
处取得极大值,在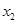 处取得极小值,满足
处取得极小值,满足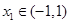 ,
,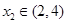 ,则
,则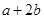 的取值范围是
的取值范围是
A.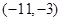 | B.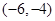 | C.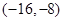 | D.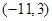 |
已知非零向量 ,
,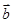 满足
满足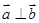 ,则函数
,则函数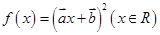 是 ( )
是 ( )
| A.偶函数 | B.奇函数 |
| C.既是奇函数又是偶函数 | D.非奇非偶函数 |
设函数 ,则在下列区间中函数
,则在下列区间中函数 不存在零点的是
不存在零点的是
A.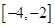 | B.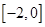 | C.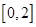 | D.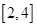 |
函数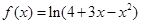 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B.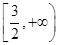 | C.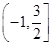 | D.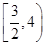 |
已知函数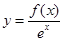 ,满足
,满足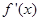 >
> ,则
,则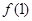 与
与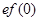 的大小关系是( )
的大小关系是( )
A.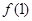 < <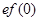 | B.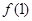 > >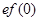 |
C.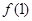 = = 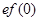 | D.不能确定 |
 ]时,f(x)=
]时,f(x)=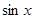 ,则f(
,则f(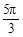 )的值为( )
)的值为( )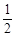
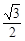
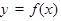 在R上可导,且满足不等式
在R上可导,且满足不等式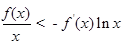 恒成立,且常数
恒成立,且常数 满足
满足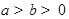 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )