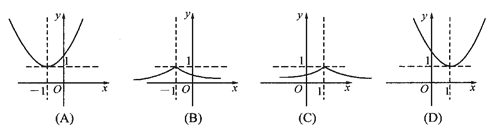
题目内容
定义在R上的函数f(x)既是偶函数又是周期函数若f(x)的最小正周期是π,且当x∈[0, ]时,f(x)=
]时,f(x)=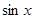 ,则f(
,则f(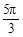 )的值为( )
)的值为( )
A.-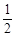 | B.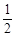 | C.-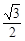 | D.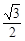 |
D
解析试题分析:要求f(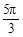 ),则必须用f(x)=sinx来求解,那么必须通过奇偶性和周期性,将变量转化到区间[0
),则必须用f(x)=sinx来求解,那么必须通过奇偶性和周期性,将变量转化到区间[0 ]上,再应用其解析式求解。解:∵f(x)的最小正周期是π,故f(
]上,再应用其解析式求解。解:∵f(x)的最小正周期是π,故f(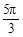 )= f(
)= f( )= f(
)= f( )∵函数f(x)是偶函数,f(
)∵函数f(x)是偶函数,f( )= f(
)= f( ),且有当x∈[0,
),且有当x∈[0, ]时,f(x)=
]时,f(x)=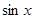 ,故可知函数值为
,故可知函数值为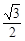 ,选D.
,选D.
考点:函数的奇偶性,周期性
点评:本题主要考查了函数的奇偶性,周期性以及应用区间上的解析性求函数值,是基础题,应熟练掌握

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四组函数,表示同一函数的是( )
A. |
B. |
C. |
D. |
用二分法计算函数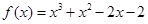 的一个正数零点的近似值(精确到0.1)为( )
的一个正数零点的近似值(精确到0.1)为( )
参考数据:
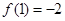 | 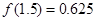 |
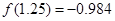 | 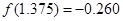 |
 | 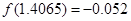 |
已知 是函数
是函数 的零点,若
的零点,若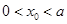 ,则
,则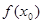 的值满足( )
的值满足( )
A.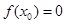 | B.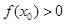 |
C.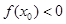 | D.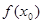 的符号不确定 的符号不确定 |
已知R上的函数y=f(x),其周期为2,且x∈(-1,1]时f(x)=1+x2,函数g(x)=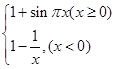 ,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
,则函数h(x)=f(x)-g(x)在区间[-5,5]上的零点的个数为( )
| A.11 | B.10 | C.9 | D.8 |
下列函数中既是奇函数,又在区间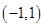 上是增函数的为( )
上是增函数的为( )
A.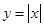 | B.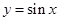 | C.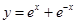 | D.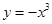 |
已知函数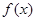 对任意
对任意 都有
都有 ,若
,若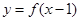 的象关于直线
的象关于直线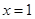 对称,且
对称,且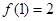 ,则
,则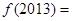 ( )
( )
| A.2 | B.3 | C.4 | D.0 |
 在定义域内可导,
在定义域内可导, 图像如图所示,则导函数
图像如图所示,则导函数 的图像可能为( )
的图像可能为( )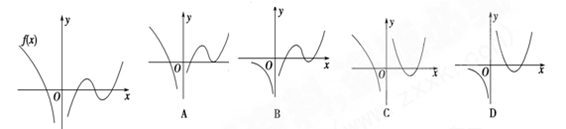
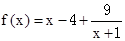 ,
,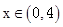 ,当
,当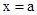 时,
时,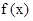 取得最小值
取得最小值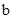 ,则函数
,则函数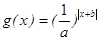 的图象为( )
的图象为( )