题目内容
 如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,
如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,(1)求证:A1E∥平面PBC;
(2)当k=
| 2 |
(3)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
分析:依题意,设此棱柱的高AA1=2,则AB=2k,以O为原点建立空间直角坐标系,写出相关点的坐标和相关向量的坐标:(1)取BC中点F,得
=
,利用线面平行的判定定理证明即可;(2)求平面PBC的法向量,利用向量夹角公式计算
与法向量夹角的余弦值,其绝对值即为线面角的正弦值;(3)利用重心坐标公式计算三角形PBC重心的坐标,可知若O在平面PBC内的射影恰好为△PBC的重心,当且仅当
•
=0,列方程即可解得k值
| PF |
| A1E |
| PA |
| OM |
| PB |
解答:解:设此棱柱的高AA1=2,则AB=2k,如图建立空间直角坐标系:
则P(0,0,2),O(0,0,0),B(k,k,0),C(-k,k,0),A1(k,-k,2),A(k,-k,0),
E(k,0,0)
∴
=(-2k,0,0),
=(k,k,-2),
=(0,k,-2),
=(k,-k,-2)
(1)取BC中点F(0,k,0)
则
=(0,k,-2)
∴
=
∴A1E∥PF,PF?面PBC,A1E?面PBC
∴A1E∥平面PBC
(2)当k=
时,∴
=(-2
,0,0),
=(
,
,-2),
=(
,-
,-2)
设平面PBC的法向量为
=(x,y,z)
则
∴取
=(0,
,1)
∴cos<
,
>=
=
=-
=-
设直线PA与平面PBC所成角为θ,则sinθ=
∴直线PA与平面PBC所成角的正弦值为
(3)设△PBC的重心坐标为M(x,y,z),则
x=
=0,y=
=
,z=
=
∴M(0,
,
)
∴
=(0,
,
)
且
•
=0,即OM⊥BC
若OM⊥平面PBC,
则
•
=
×k+
×(-2)=0
解得k=±
∴k=±
时,O在平面PBC内的射影恰好为△PBC的重心

则P(0,0,2),O(0,0,0),B(k,k,0),C(-k,k,0),A1(k,-k,2),A(k,-k,0),
E(k,0,0)
∴
| BC |
| PB |
| A1E |
| PA |
(1)取BC中点F(0,k,0)
则
| PF |
∴
| PF |
| A1E |
∴A1E∥PF,PF?面PBC,A1E?面PBC
∴A1E∥平面PBC
(2)当k=
| 2 |
| BC |
| 2 |
| PB |
| 2 |
| 2 |
| PA |
| 2 |
| 2 |
设平面PBC的法向量为
| n |
则
|
∴取
| n |
| 2 |
∴cos<
| PA |
| n |
| ||||
|
|
| 0-2-2 | ||||
|
| 2 | ||
|
| ||
| 3 |
设直线PA与平面PBC所成角为θ,则sinθ=
| ||
| 3 |
∴直线PA与平面PBC所成角的正弦值为
| ||
| 3 |
(3)设△PBC的重心坐标为M(x,y,z),则
x=
| 0+k-k |
| 3 |
| 0+k+k |
| 3 |
| 2k |
| 3 |
| 2+0+0 |
| 3 |
| 2 |
| 3 |
∴M(0,
| 2k |
| 3 |
| 2 |
| 3 |
∴
| OM |
| 2k |
| 3 |
| 2 |
| 3 |
且
| OM |
| BC |
若OM⊥平面PBC,
则
| OM |
| PB |
| 2k |
| 3 |
| 2 |
| 3 |
解得k=±
| 2 |
∴k=±
| 2 |
点评:本题综合考查了线面平行的判定定理,线面垂直的判定定理,利用空间向量和空间直角坐标系求空间直线与平面所成的角的方法

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆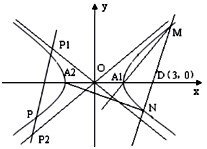 (2010•上饶二模)如图,已知P是焦距为上一点,过P的直线与双曲线C的两条渐近线分别交于点P1,P2,且
(2010•上饶二模)如图,已知P是焦距为上一点,过P的直线与双曲线C的两条渐近线分别交于点P1,P2,且
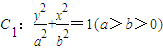 的上、下焦点,其中F1也是抛物线
的上、下焦点,其中F1也是抛物线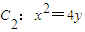 的焦点,点M是C1与C2在第二象限的交点,且
的焦点,点M是C1与C2在第二象限的交点,且 .
.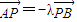 ,
,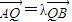 (λ≠0且λ≠±1),
(λ≠0且λ≠±1),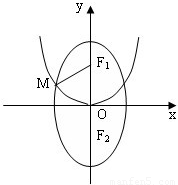
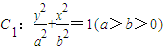 的上、下焦点,其中F1也是抛物线
的上、下焦点,其中F1也是抛物线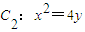 的焦点,点M是C1与C2在第二象限的交点,且
的焦点,点M是C1与C2在第二象限的交点,且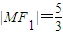 .
.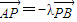 ,
,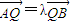 (λ≠0且λ≠±1),
(λ≠0且λ≠±1),