题目内容
如图,已知F1、F2分别为椭圆![]() 的上、下焦点,其中F1也是抛物线C2∶x2=4y的焦点,点M是C1与C2在第二象限的交点,且
的上、下焦点,其中F1也是抛物线C2∶x2=4y的焦点,点M是C1与C2在第二象限的交点,且![]()
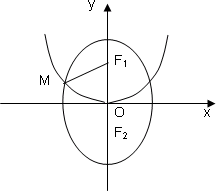
(I)求椭圆C1的方程;
(II)已知点P(1,3)和圆O∶x2+y2=b2,过点P的动直线l与圆O相交于不同的两点A,B,在线段AB上取一点Q,满足∶![]() ,
,![]() (λ≠0且λ≠±1),求证∶点Q总在某条定直线上.
(λ≠0且λ≠±1),求证∶点Q总在某条定直线上.
答案:
解析:
解析:
(1)解法一∶令M为![]() ,因为M在抛物线
,因为M在抛物线![]() 上,
上,
故![]() ,①又
,①又![]() ,则
,则![]() ②
②
由①②解得![]() ,
,![]()
椭圆![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,点M在椭圆上,由椭圆定义,得
,点M在椭圆上,由椭圆定义,得![]()
![]()
![]() ,又
,又![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
解法二∶同上求得M,而点M在椭圆上,故有 ,即
,即![]()
又![]() ,即
,即![]() ,解得
,解得![]()
![]() 椭圆
椭圆![]() 的方程为
的方程为![]()
(2)证明∶设![]() ,
,![]() ,
,![]()
由![]() ,可得
,可得![]()
即
由![]() ,可得
,可得![]()
即
⑤×⑦得![]() , ⑥×⑧得
, ⑥×⑧得![]()
两式相加,得![]()
又点A,B在圆![]() 上,
上,![]() ,且
,且![]()
即![]() ,故点Q总在直线
,故点Q总在直线![]() 上
上


练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C: (2012•鹰潭一模)如图,已知F1,F2是椭圆
(2012•鹰潭一模)如图,已知F1,F2是椭圆 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆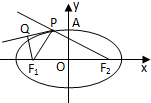 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆