题目内容
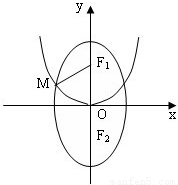
如图,已知F1、F2分别为椭圆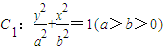 的上、下焦点,其中F1也是抛物线
的上、下焦点,其中F1也是抛物线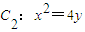 的焦点,点M是C1与C2在第二象限的交点,且
的焦点,点M是C1与C2在第二象限的交点,且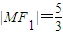 .
.(1)求椭圆C1的方程;
(2)已知点P(1,3)和圆O:x2+y2=b2,过点P的动直线l与圆O相交于不同的两点A,B,在线段AB上取一点Q,满足:
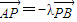 ,
,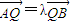 (λ≠0且λ≠±1),
(λ≠0且λ≠±1),求证:点Q总在某条定直线上.
【答案】分析:(1)解法一:利用抛物线的方程和定义即可求出点M的坐标,再利用椭圆的定义即可求出;
解法二:同解法一求出点M的坐标,再利用椭圆的标准方程及参数a,b,c的关系即可求出.
(2)方法一:利用已知向量相等及点A,B在圆上满足圆的方程即可证明;
方法二:利用向量相等、直线与圆相交问题得到根与系数的关系即可证明.
解答:解:(1)解法一:令M为(x,y),因为M在抛物线C2上,故 ,①
,①
又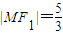 ,则
,则 ②
②
由①②解得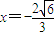 ,
,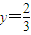
椭圆C1的两个焦点为F1(0,1),F2(0,-1),点M在椭圆上,由椭圆定义,得2a=|MF1|+|MF2|=
∴a=2,又c=1,∴b2=a2-c2=3
∴椭圆C1的方程为 .
.
解法二:同上求得M,而点M在椭圆上,故有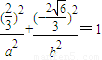 ,即
,即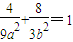 ,
,
又c=1,即b2=a2-1,解得a2=4,b2=3∴椭圆C1的方程为 .
.
(2)证明:方法一:设A(x1,y1),B(x2,y2),Q(x,y)
由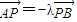 ,可得(1-x1,3-y1)=-λ(x2-1,y2-3),
,可得(1-x1,3-y1)=-λ(x2-1,y2-3),
即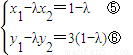
由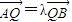 ,可得(x-x1,y-y1)=λ(x2-x,y2-y),
,可得(x-x1,y-y1)=λ(x2-x,y2-y),

⑤×⑦得 ,⑥×⑧得
,⑥×⑧得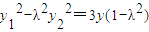
两式相加,得
又点A,B在圆x2+y2=3上,∴ ,且λ≠±1
,且λ≠±1
即x+3y=3,故点Q总在直线x+3y=3上
方法二:
由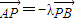 ,可得(1-x1,3-y1)=-λ(x2-1,y2-3),∴
,可得(1-x1,3-y1)=-λ(x2-1,y2-3),∴ ,
,
由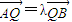 ,可得(x-x1,y-y1)=λ(x2-x,y2-y),∴
,可得(x-x1,y-y1)=λ(x2-x,y2-y),∴ ,
,
∴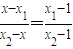 ,∴
,∴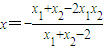 (*)
(*)
当斜率不存在时,由特殊情况得到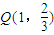 ,
,
当斜率存在时,设直线为y=k(x-1)+3 ,
,
∴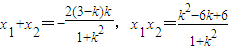 ,
,
代入(*)得 ,而y=k(x-1)+3,消去k,得x+3y=3
,而y=k(x-1)+3,消去k,得x+3y=3
而 满足方程,∴Q在直线x+3y=3上.
满足方程,∴Q在直线x+3y=3上.
点评:熟练掌握圆锥曲线的定义和性质、向量相等、直线与圆锥曲线的相交问题及根与系数的关系是解题的关键.本题需要较强的计算能力,注意分类讨论的思想方法应用.
解法二:同解法一求出点M的坐标,再利用椭圆的标准方程及参数a,b,c的关系即可求出.
(2)方法一:利用已知向量相等及点A,B在圆上满足圆的方程即可证明;
方法二:利用向量相等、直线与圆相交问题得到根与系数的关系即可证明.
解答:解:(1)解法一:令M为(x,y),因为M在抛物线C2上,故
 ,①
,①又
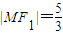 ,则
,则 ②
②由①②解得
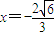 ,
,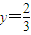
椭圆C1的两个焦点为F1(0,1),F2(0,-1),点M在椭圆上,由椭圆定义,得2a=|MF1|+|MF2|=

∴a=2,又c=1,∴b2=a2-c2=3
∴椭圆C1的方程为
 .
.解法二:同上求得M,而点M在椭圆上,故有
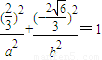 ,即
,即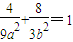 ,
,又c=1,即b2=a2-1,解得a2=4,b2=3∴椭圆C1的方程为
 .
.(2)证明:方法一:设A(x1,y1),B(x2,y2),Q(x,y)
由
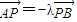 ,可得(1-x1,3-y1)=-λ(x2-1,y2-3),
,可得(1-x1,3-y1)=-λ(x2-1,y2-3),即
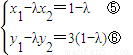
由
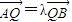 ,可得(x-x1,y-y1)=λ(x2-x,y2-y),
,可得(x-x1,y-y1)=λ(x2-x,y2-y),
⑤×⑦得
 ,⑥×⑧得
,⑥×⑧得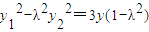
两式相加,得

又点A,B在圆x2+y2=3上,∴
 ,且λ≠±1
,且λ≠±1即x+3y=3,故点Q总在直线x+3y=3上
方法二:
由
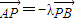 ,可得(1-x1,3-y1)=-λ(x2-1,y2-3),∴
,可得(1-x1,3-y1)=-λ(x2-1,y2-3),∴ ,
,由
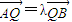 ,可得(x-x1,y-y1)=λ(x2-x,y2-y),∴
,可得(x-x1,y-y1)=λ(x2-x,y2-y),∴ ,
,∴
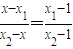 ,∴
,∴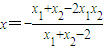 (*)
(*)当斜率不存在时,由特殊情况得到
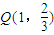 ,
,当斜率存在时,设直线为y=k(x-1)+3
 ,
,∴
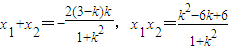 ,
,代入(*)得
 ,而y=k(x-1)+3,消去k,得x+3y=3
,而y=k(x-1)+3,消去k,得x+3y=3而
 满足方程,∴Q在直线x+3y=3上.
满足方程,∴Q在直线x+3y=3上.点评:熟练掌握圆锥曲线的定义和性质、向量相等、直线与圆锥曲线的相交问题及根与系数的关系是解题的关键.本题需要较强的计算能力,注意分类讨论的思想方法应用.

练习册系列答案
相关题目
 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C: (2012•鹰潭一模)如图,已知F1,F2是椭圆
(2012•鹰潭一模)如图,已知F1,F2是椭圆 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆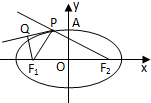 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆