题目内容
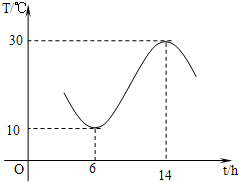 武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
(Ⅰ)写出这段曲线的函数解析式;
(Ⅱ)求出一天(t∈[0,24],单位小时)温度的变化在[20,25]时的时间.
解:(Ⅰ)由条件可知 解得
解得 ,
,
因为 ×
× =14-6,所以ω=
=14-6,所以ω= ,
,
∴y=10sin( x+φ)+20;
x+φ)+20;
将点(6,10)代入上式,得φ= .
.
∴解析式是y=10sin( x+
x+ )+20.…(6分)
)+20.…(6分)
(Ⅱ)由(Ⅰ),令20≤10sin( x+
x+ )+20≤25,
)+20≤25,
得0≤sin( x+
x+ )≤
)≤ .
.
∴2kπ≤ x+
x+ ≤2kπ+
≤2kπ+ ,…①
,…①
或2kπ+ ≤
≤ x+
x+ ≤2kπ+π,…②
≤2kπ+π,…②
由①得16k-6≤x≤16k-6+ .取k=1,得10≤x≤11+
.取k=1,得10≤x≤11+ .
.
由②得16k+ ≤x≤16k+2.取k=0,得
≤x≤16k+2.取k=0,得 ≤x≤2;
≤x≤2;
取k=1,得16+ ≤x≤18.
≤x≤18.
即一天温度的变化在[20,25]时的时间是0:40~2:00,10:00~11:20,16:40~18:00三个时间段,共4小时…(12分)
分析:(Ⅰ)由题意可得 ,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式;
,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式;
(Ⅱ)依题意可得0≤sin( x+
x+ )≤
)≤ ,结合正弦函数的图象与性质有2kπ≤
,结合正弦函数的图象与性质有2kπ≤ x+
x+ ≤2kπ+
≤2kπ+ ,或2kπ+
,或2kπ+ ≤
≤ x+
x+ ≤2kπ+π,分别对k赋值即可求得答案.
≤2kπ+π,分别对k赋值即可求得答案.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查三角函数的图象与性质,赋值法的应用是难点,属于中档题.
 解得
解得 ,
,因为
 ×
× =14-6,所以ω=
=14-6,所以ω= ,
,∴y=10sin(
 x+φ)+20;
x+φ)+20;将点(6,10)代入上式,得φ=
 .
.∴解析式是y=10sin(
 x+
x+ )+20.…(6分)
)+20.…(6分)(Ⅱ)由(Ⅰ),令20≤10sin(
 x+
x+ )+20≤25,
)+20≤25,得0≤sin(
 x+
x+ )≤
)≤ .
.∴2kπ≤
 x+
x+ ≤2kπ+
≤2kπ+ ,…①
,…①或2kπ+
 ≤
≤ x+
x+ ≤2kπ+π,…②
≤2kπ+π,…②由①得16k-6≤x≤16k-6+
 .取k=1,得10≤x≤11+
.取k=1,得10≤x≤11+ .
.由②得16k+
 ≤x≤16k+2.取k=0,得
≤x≤16k+2.取k=0,得 ≤x≤2;
≤x≤2;取k=1,得16+
 ≤x≤18.
≤x≤18.即一天温度的变化在[20,25]时的时间是0:40~2:00,10:00~11:20,16:40~18:00三个时间段,共4小时…(12分)
分析:(Ⅰ)由题意可得
 ,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式;
,从而可求得A,b,再有函数图象可知其周期为16,从而可求得ω,进一步可求得φ,于是可求得这段曲线的函数解析式;(Ⅱ)依题意可得0≤sin(
 x+
x+ )≤
)≤ ,结合正弦函数的图象与性质有2kπ≤
,结合正弦函数的图象与性质有2kπ≤ x+
x+ ≤2kπ+
≤2kπ+ ,或2kπ+
,或2kπ+ ≤
≤ x+
x+ ≤2kπ+π,分别对k赋值即可求得答案.
≤2kπ+π,分别对k赋值即可求得答案.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查三角函数的图象与性质,赋值法的应用是难点,属于中档题.

练习册系列答案
相关题目
 (2012•武昌区模拟)武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).
(2012•武昌区模拟)武汉地区春天的温度的变化曲线近似地满足函数y=Asin(ωx+φ)+b(如图所示,单位:摄氏温度,A>0,ω>0,0<φ<π).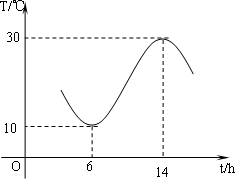
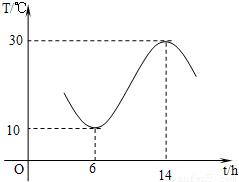
 (如图所示,单位:摄氏温度,
(如图所示,单位:摄氏温度, ).
).
 ,单位小时)
,单位小时) 时的时间.
时的时间.