题目内容
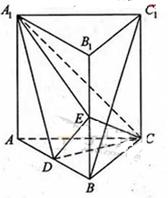
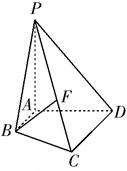
如图,在四面体 中,
中,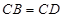 ,
,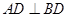 ,点
,点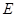 ,
,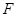 分别是
分别是 ,
, 的中点.
的中点.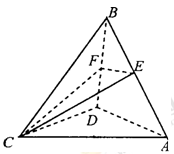
(1)EF∥平面ACD;
(2)求证:平面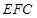 ⊥平面
⊥平面 ;
;
(3)若平面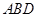 ⊥平面
⊥平面 ,且
,且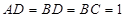 ,求三棱锥
,求三棱锥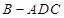 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)
解析试题分析:(1)由直线和平面平行的判定定理,只需在平面内找一条直线与平面外直线平行,由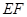 是
是 的中位线,知
的中位线,知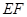 ∥
∥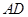 ;(2)由平面和平面垂直的判定定理,只需在一个平面内找另一个平面的垂线即可,由
;(2)由平面和平面垂直的判定定理,只需在一个平面内找另一个平面的垂线即可,由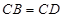 且
且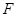 是
是 的中点,可得
的中点,可得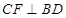 ,又
,又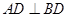 且
且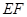 ∥
∥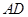 ,知
,知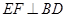 ,且
,且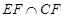 =
=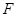 ,所以
,所以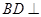 面
面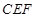 ,又
,又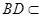 面
面 ,从而平面
,从而平面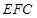 ⊥平面
⊥平面 ;(3)由已知面
;(3)由已知面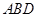 ⊥平面
⊥平面 ,则在一个平面内垂直于交线的直线,必垂直于另一个平面,由面
,则在一个平面内垂直于交线的直线,必垂直于另一个平面,由面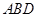
 平面
平面 =
= ,且
,且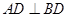 ,所以
,所以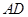
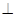 面
面 ,∴
,∴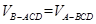 ,只需求
,只需求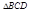 的面积即可.
的面积即可.
试题解析:(1)∵EF是△BAD的中位线,所以EF∥AD(2分),又EF?平面ACD,AD?平面ACD
∴EF∥平面ACD;
(2)∵EF∥AD,AD⊥BD,∴BD⊥EF,又∵BD⊥CF∴BD⊥面CEF,又BD?面BDC,∴面EFC⊥面BCD;
(3)因为面ABD⊥面BCD,且AD⊥BD,所以AD⊥面BCD,由BD=BC=1和CB=CD得△BCD是正三角形,所以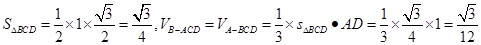 .
.
考点:1、直线和平面平行的判定定理;2、面面垂直的判定和性质定理;3、几何体的体积.

练习册系列答案
相关题目
 平面
平面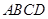 ,四边形
,四边形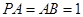 ,
,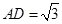 ,点
,点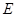 ,
,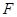 分别是
分别是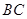 ,
,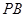 的中点.
的中点.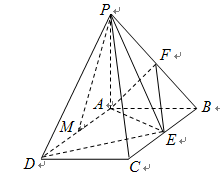
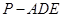 的体积;
的体积; 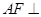 平面
平面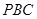 ;
;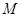 为线段
为线段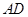 中点,求证:
中点,求证: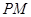 ∥平面
∥平面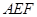 .
.
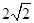 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.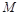 是
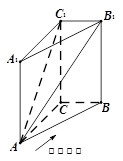
是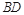 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.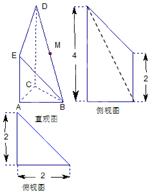
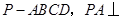 平面
平面 ,底面
,底面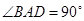 ,且
,且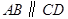 ,
,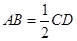 .
.
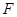 在线段
在线段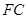 上运动,且设
上运动,且设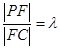 ,问当
,问当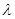 为何值时,
为何值时,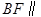 平面
平面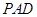 ,并证明你的结论;
,并证明你的结论;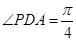 ,
,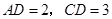 求四棱锥
求四棱锥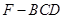 的体积.
的体积.
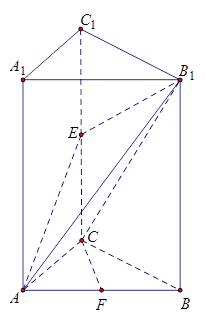
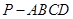 中,
中,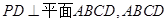 是正方形,E是
是正方形,E是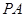 的中点,
的中点,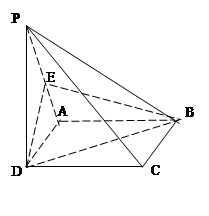
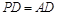 ,求 PC与面AC所成的角
,求 PC与面AC所成的角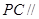 平面
平面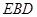
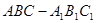 的三视图和直观图如图所示.
的三视图和直观图如图所示.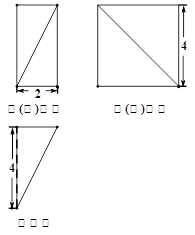
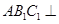 平面
平面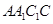 ;
;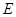 是线段
是线段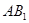 上的一点,且满足
上的一点,且满足 ,求
,求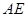 的长.
的长.