题目内容
 已知椭圆E:
已知椭圆E:| x2 | 4 |
4
4
.分析:设椭圆E的内接平行四边形为如图的四边形ABCD,根据椭圆方程算出两个焦点的坐标,从而设AB方程为y=k(x+
),与椭圆方程联解消去y得(1+4k2)x-8
k2x+4(3k2-1)=0,设A(x1,y1)、B(x2,y2),利用根与系数的关系与弦长公式算出|AB|=
.设CD方程为y=k(x-
),利用平行线的距离公式算出直线AB、CD的距离为d=
,从而得到平行四边形ABCD的面积S=|AB|×d=8
•
.最后采用换元法结合基本不等式求最值,即可求出当且仅当k=±
时,平行四边形ABCD的面积S取得最大值为4.
| 3 |
| 3 |
| 4(1+k2) |
| 1+4k2 |
| 3 |
2
| ||
|
| 3 |
|
| ||
| 2 |
解答:解: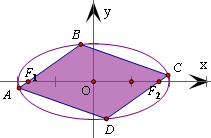 根据椭圆E方程,可得焦点坐标分别为F1(-
根据椭圆E方程,可得焦点坐标分别为F1(-
,0),F2(
,0)
设椭圆E的内接平行四边形为四边形ABCD,如图所示
直线AB方程为y=k(x+
),直线CD方程为y=k(x-
),
则由
消去y,得(1+4k2)x-8
k2x+4(3k2-1)=0
设A(x1,y1),B(x2,y2),可得
由此可得|x1-x2|=
=
∴|AB|=
|x1-x2|=
由平行线之间的距离公式,得直线AB、CD的距离为d=
因此,平行四边形ABCD的面积S=|AB|×d=8
•
令t=
=
+
=
+
再令
k2-
=s,显然当k2>
时,s>0,t=
+
>
,此时可取到最大值.
∵t=
+
=
+
≤
+
=
∴平行四边形ABCD的面积S=8
•
≤8
×
=4,
当且仅当k=±
时,平行四边形ABCD的面积S取得最大值为4
故答案为:4
 根据椭圆E方程,可得焦点坐标分别为F1(-
根据椭圆E方程,可得焦点坐标分别为F1(-| 3 |
| 3 |
设椭圆E的内接平行四边形为四边形ABCD,如图所示
直线AB方程为y=k(x+
| 3 |
| 3 |
则由
|
| 3 |
设A(x1,y1),B(x2,y2),可得
|
由此可得|x1-x2|=
| (x1+x2)2-4x 1x2 |
4
| ||
| 1+4k2 |
∴|AB|=
| 1+k2 |
| 4(1+k2) |
| 1+4k2 |
由平行线之间的距离公式,得直线AB、CD的距离为d=
2
| ||
|
因此,平行四边形ABCD的面积S=|AB|×d=8
| 3 |
|
令t=
| k2(1+k2) |
| (1+4k2)2 |
(
| ||
| (1+4k2)2 |
| ||||
| (1+4k2)2 |
| 1 |
| 16 |
| ||||
| (1+4k2)2 |
再令
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 16 |
| ||||
| (1+4k2)2 |
| 1 |
| 16 |
∵t=
| 1 |
| 16 |
| s | ||
64s2+24s+
|
| 1 |
| 16 |
| 1 | ||
24+(64s +
|
| 1 |
| 16 |
| 1 | ||||
24+2
|
| 1 |
| 12 |
∴平行四边形ABCD的面积S=8
| 3 |
| t |
| 3 |
|
当且仅当k=±
| ||
| 2 |
故答案为:4
点评:本题给出椭圆的内接平行四边形,在已知两个焦点在平行四边形的对边上时,求平行四边形面积的最大值,着重考查了椭圆的简单几何性质、直线与圆锥曲线位置关系和利用基本不等式求最值等知识,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C:
圆锥曲线上任意两点连成的线段称为弦.若圆锥曲线上的一条弦垂直于其对称轴,我们将该弦称之为曲线的垂轴弦.已知椭圆C: (2013•江苏一模)已知椭圆
(2013•江苏一模)已知椭圆 已知椭圆
已知椭圆