题目内容

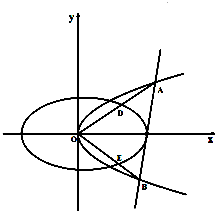已知椭圆C1：
x2
4
+
y2
3
=1，抛物线C2：y2=4x，过椭圆C1右顶点的直线l交抛物线C2于A，B两点，射线OA，OB分别与椭圆交于点D，E，点O为原点．
（Ⅰ）求证：点O在以DE为直径的圆的内部；
（Ⅱ）记△ODE，△OAB的面积分别为S1，S2，问是否存在直线l使S2=3S1？若存在，求出直线l的方程，若不存在，请说明理由．
分析：（1）设A（x1，y1），B（x2，y2），直线l：x=my+2，代入y2=4x，根据方程的根与系数关系可求y1+y2，y1y2，要证明点O在以DE为直径的圆的内部；只要证明
OA
•
OB
＜0即可
（2）设D（x3，y3），E（x4，y4），则射线OA：y=
4
y1
x，代入
x2
4
+
y2
3
=1得y32=
64×3
3y12+64
，同理可得y42=
64×3
3y22+64
，代入检验即可验证
解答：（1）证明：设直线l：x=my+2，代入y2=4x得y2-4my-8=0
设A（x1，y1），B（x2，y2）
∴y1+y2=4m，y1y2=-8，x1x2=（my1+2）（my2+2）=m2y1y2+2m（y1+y2）+4
∴
OA
•
OB
=x1x2+y1y2=(1+m2)y1y2+2m(y1+y2)+4=-4＜0
∴∠AOB＞90°即∠DOE＞90°
∴点O在以DE为直径的圆的内部
（2）设D（x3，y3），E（x4，y4）
则射线OA：y=
4
y1
x，代入
x2
4
+
y2
3
=1得y32=
64×3
3y12+64
，
同理y42=
64×3
3y22+64

∴(
s2
s1
)2=(
|y1y2|
|y3y4|
)2=
64
64×3
3y12+64
•
64×3
3y22+64
=
(3y12+64)(3y22+64)
64×9

=
73+3[(y1+y2)2-2y1y2]
9

=
73+3(16m2+16)
9

=
121+48m2
9
=9
∴m2=-
5
6

故不存在满足条件的直线l
点评：本题主要考查了直线与抛物线的 相交关系的应用，方程的根与系数关系的应用，属于综合性试题
练习册系列答案
相关题目
已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．
已知椭圆C1：
x24
+y2=1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
（1）求椭圆C2的方程；
（2）设O为坐标原点，过O的直线l与C1相交于A，B两点，且l与C2相交于C，D两点．若|CD|=2|AB|，求直线l的方程．
已知椭圆C1：
x2
4
+y2=1，椭圆C2以椭圆C1的长轴为短轴，且与C1有相同的离心率，则椭圆C2的标准方程为
y2
16
+
x2
4
=1
y2
16
+
x2
4
=1
．
已知椭圆C1：
x2
4
+
y2
3
=1，其左准线为l1，右准线为l2，一条以原点为顶点，l1为准线的抛物线C2交l2于A，B两点，则|AB|等于（　　）
A、2B、4C、8D、16
如图，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似的，则称这两个椭圆是“相似椭圆”，且三角形的相似比即为椭圆的相似比．
（1）已知椭圆C1：
x2
4
+y2=1和C2：
x2
16
+
y2
4
=1判断C2与C1是否相似，如果相似则求出C2与C1的相似比，若不相似请说明理由；
（2）写出与椭圆C1相似且半短轴长为b的椭圆Cb的方程，并列举相似椭圆之间的三种性质（不需证明）；
（3）已知直线l：y=x+1，在椭圆Cb上是否存在两点M、N关于直线l对称，若存在，则求出函数f（b）=|MN|的解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网