题目内容
将长度为 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这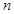 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时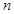 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时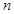 的最大值为4.则:
的最大值为4.则:
(1)当 时,
时,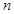 的最大值为________;(2)当
的最大值为________;(2)当 时,
时,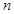 的最大值为________.
的最大值为________.
 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这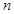 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时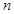 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时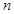 的最大值为4.则:
的最大值为4.则:(1)当
 时,
时,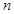 的最大值为________;(2)当
的最大值为________;(2)当 时,
时,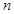 的最大值为________.
的最大值为________.(1)5;(2)9.
试题分析:当
 时,
时,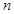 的最大值为3;当
的最大值为3;当 时,可以分为1,1,2,3的四段,此时
时,可以分为1,1,2,3的四段,此时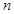 的最大值为4;接着
的最大值为4;接着  时,可以分为1,1,2, 3,,5的四段,
时,可以分为1,1,2, 3,,5的四段,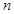 的最大值为5;依次数列变为1,1,2,3,5,8,13,21,34此时线段长度为88,
的最大值为5;依次数列变为1,1,2,3,5,8,13,21,34此时线段长度为88,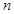 的最大值为9,当
的最大值为9,当 依次数列变为1,1,2,3,5,8,13,21,34,46,
依次数列变为1,1,2,3,5,8,13,21,34,46, 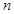 的最大值为9.
的最大值为9.
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 与它的高
与它的高 的关系是:
的关系是: ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径 的前
的前 项和为
项和为 .若数列
.若数列 则
则 若存在正整数
若存在正整数 ,使
,使
 ,则
,则
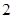 、
、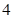 、
、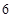 、
、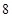 、
、 按表
按表 的方式进行排列,记
的方式进行排列,记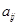 表示第
表示第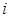 行和第
行和第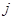 列的数,若
列的数,若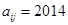 ,则
,则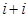 的值为( )
的值为( )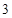 列
列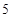 列
列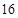
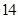
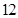
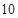
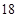
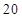
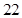
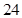
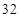
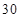
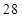
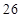
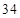
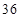
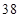
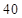
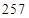 B.
B.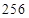 C.
C.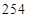 D.
D.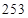
 (n≥2),每个数是它下一行左右相邻两数的和,如
(n≥2),每个数是它下一行左右相邻两数的和,如 =
= +
+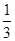 +
+ ,
, +
+ ,则第10行第4个数(从左往右数)为( )
,则第10行第4个数(从左往右数)为( )
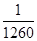



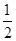 ,an+1=
,an+1= ,则a2,a3,a4,a5的值分别为________________,由此猜想an=________.
,则a2,a3,a4,a5的值分别为________________,由此猜想an=________.