题目内容

以下结论正确的一项是（　　）
分析：由一次函数的单调性，可判断A，由反比例函数的单调性，可判断B；由二次函数的单调性，可判断C；由对勾函数的单调性，可判断D．
解答：解：由一次函数的性质，当k＞0，则y=kx+b是R上增函数，故A错误；
由反比例函数的性质，当k＞0，则y=
k
x
是（0，+∞）上减函数，故B正确；
由二次函数的性质，当a＞0时，y=ax2+bx+c在（-∞，-
b
2a
]上是减函数，在[-
b
2a
，+∞）上是增函数，故C错误；
由对勾函数的性质，当k＞0，则y=x+
k
x
在（0，
k
]上是减函数，在[
k
，+∞）上增函数，故D错误
故选B
点评：本题以命题的真假判断为载体考查了函数的单调性，熟练掌握各种基本初等函数的单调性是解答的关键．
练习册系列答案
相关题目
（2012•资阳一模）已知一非零向量数列{
a
n}满足
a
1=（1，1）
a
n=(xn，yn)=
1
2
(xn-1-yn-1，xn-1+yn-1)（n≥2且n∈N*）．给出以下结论：
①数列{|
a
n|}是等差数列；
②|
a
1|•|
a
5|=
1
2
；
③设cn=2log2|
a
n|，则数列{cn}的前n项和为Tn，当且仅当n=2时，Tn取得最大值；
④记向量
a
n与
a
n-1的夹角为θn（n≥2），均有θn=
π
4
．其中所有正确结论的序号是
②④
②④
．
已知一非零向量数列{an}满足a1=（1，1）an=(xn，yn)=
1
2
(xn-1-yn-1，xn-1+yn-1)（n≥2且n∈N*）．给出以下结论：
①数列{|an|}是等差数列，②|a1|•|a5|=
1
2
；③设cn=2log2|an|，则数列{cn}的前n项和为Tn，当且仅当n=2时，Tn取得最大值；④记向量an与an-1的夹角为θn（n≥2），均有θn=
π
4
．其中所有正确结论的序号是
 
．

已知一非零向量数列满足。给出以下结论：

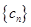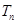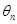1．数列是等差数列，2。；3。设，则数列的前n项和为,当且仅当n=2时，取得最大值；4。记向量与的夹角为（），均有。其中所有正确结论的序号是____

 
以下结论正确的一项是（ ）
A．若k＞0，则y=kx+b是R上减函数
B．k＞0，则y=是（0，+∞）上减函数
C．若a＞0，则y=ax2+bx+c是R上增函数
D．k＞0，y=x+是（0，+∞）上增函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网