题目内容
 如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为
如图,PA切⊙O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60°到OD,则PD的长为分析:解法一:如图根据题设条件可求得角DOP的大小,由于OD=1,OP=2,由余弦定理求长度即可.
解法二:由图形知,若能求得点D到线段OC的距离DE与线段OE的长度,在直角三角形PED中用勾股定理求PD即可.
解法二:由图形知,若能求得点D到线段OC的距离DE与线段OE的长度,在直角三角形PED中用勾股定理求PD即可.
解答: 解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,
解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,
∴∠AOB=60°,∴∠POD=120°,
在△POD中由余弦定理,
得:PD2=PO2+DO2-2PO•DOcos∠POD=4+1-4×(-
)=7.
∴PD=
.
法二:过点D作DE⊥PC垂足为E,
∵∠POD=120°,
∴∠DOC=60°,
可得OE=
,DE=
,
在Rt△PED中,有
PD=
=
=
.
 解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,
解:法一:∵PA切⊙O于点A,B为PO中点,∴AB=OB=OA,∴∠AOB=60°,∴∠POD=120°,
在△POD中由余弦定理,
得:PD2=PO2+DO2-2PO•DOcos∠POD=4+1-4×(-
| 1 |
| 2 |
∴PD=
| 7 |
法二:过点D作DE⊥PC垂足为E,
∵∠POD=120°,
∴∠DOC=60°,
可得OE=
| 1 |
| 2 |
| ||
| 2 |
在Rt△PED中,有
PD=
| PE2+DE2 |
|
| 7 |
点评:本题考点是与圆有关的比例线段,本题考查求线段的长度,平面几何中求线段长度一般在三角形中用正弦定理与余弦定理求解,本题中法一的特征用的是余弦定理求长度,法二在直角三角形中用勾股定理求长度,在三角形中求长度时应该根据题意选取适当的方法求解,做题后要注意总结方法选取的规律.

练习册系列答案
相关题目
 如图,PA切⊙O于点A,PA=4,PBC过圆心0,且与圆相交于B、C两点,AB:AC=1:2,则⊙O的半径为
如图,PA切⊙O于点A,PA=4,PBC过圆心0,且与圆相交于B、C两点,AB:AC=1:2,则⊙O的半径为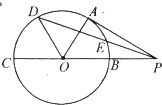 如图,PA切⊙O于点A,割线PBC经过O,OB=PB=1,0A绕着点0逆时针旋转60°到0D,PD交⊙O于点E则PE的长为
如图,PA切⊙O于点A,割线PBC经过O,OB=PB=1,0A绕着点0逆时针旋转60°到0D,PD交⊙O于点E则PE的长为 (2011•大连二模)选修4-1:几何证明选讲
(2011•大连二模)选修4-1:几何证明选讲 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.