题目内容
在锐角△ABC中,已知内角A、B、C所对的边分别为a、b、c,且(1)若a2-ab=c2-b2,求A、B、C的大小;
(2)已知向量m=(sinA,cosA),n=(cosB,sinB),求|3m-2n|的取值范围.
解:∵![]() (tanA-tanB)=1+tanA·tanB,又△ABC为锐角三角形,
(tanA-tanB)=1+tanA·tanB,又△ABC为锐角三角形,
∴![]() .∴tan(A-B)=
.∴tan(A-B)=![]() .
.
∵0<A<![]() ,0<B<
,0<B<![]() ,∴-
,∴-![]() <A-B<
<A-B<![]() .∴A-B=
.∴A-B=![]() .
.
(1)∵a2-ab=c2-b2,∴cosC=![]() .∴C=
.∴C=![]() .
.
由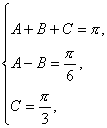 解得A=
解得A=![]() ,B=
,B=![]() .∴A=
.∴A=![]() ,B=
,B=![]() ,C=
,C=![]() .
.
(2)|3m-2n|2=9m2+4n2-12m·n=13-12(sinAcosB+cosAsinB)=13-12sin(A+B)=13-12sin(2B+![]() ).
).
∵△ABC为锐角三角形,A-B=![]() ,∴C=π-A-B<
,∴C=π-A-B<![]() ,A=
,A=![]() +B<
+B<![]() .∴
.∴![]() <B<
<B<![]() ,
,![]() <2B+
<2B+![]() <
<![]() .∴sin(2B+
.∴sin(2B+![]() )∈(
)∈(![]() ,1).
,1).
∴|3m-2n|2∈(1,7).
∴|3m-2n|的取值范围是(1,![]() ).
).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目