题目内容
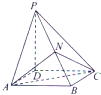 四棱锥P-ABCD的底面ABCD为正方形,且PD垂直于底面ABCD,N为PB中点,则三棱锥P-ANC与四棱锥P-ABCD的体积比为________.
四棱锥P-ABCD的底面ABCD为正方形,且PD垂直于底面ABCD,N为PB中点,则三棱锥P-ANC与四棱锥P-ABCD的体积比为________.
1:4
分析:根据几何体的结构特征,可以先求出三棱锥N-ABC与四棱锥P-ABCD的体积比,两者面积之比为2:1,高之比为2:1.
解答: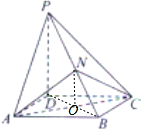 解:如图,设O为正方形ABCD中心,连接NO,由于N为PB中点,所以PD∥NO,
解:如图,设O为正方形ABCD中心,连接NO,由于N为PB中点,所以PD∥NO,
∵PD⊥底面ABCD,∴NO⊥底面ABCD,设PD=h,正方形ABCD面积为S,则VP-ABCD=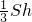 ,
,
VN-ABC= ×
×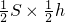 =
=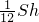 ,
,
所以VN-ABC:VP-ABCD= ,
,
同理可求得VP-ADC:VP-ABCD=1:2
所以V P-ANC:VP-ABCD=1- -
- =
=
故答案为:1:4
点评:本题考查空间几何体的体积度量、间接法解决问题.化不规则几何体为规则几何体,化不熟悉为熟悉间接求解,也是解决空间几何体体积的重要方法.
分析:根据几何体的结构特征,可以先求出三棱锥N-ABC与四棱锥P-ABCD的体积比,两者面积之比为2:1,高之比为2:1.
解答:
 解:如图,设O为正方形ABCD中心,连接NO,由于N为PB中点,所以PD∥NO,
解:如图,设O为正方形ABCD中心,连接NO,由于N为PB中点,所以PD∥NO,∵PD⊥底面ABCD,∴NO⊥底面ABCD,设PD=h,正方形ABCD面积为S,则VP-ABCD=
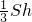 ,
,VN-ABC=
 ×
×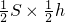 =
=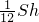 ,
,所以VN-ABC:VP-ABCD=
 ,
,同理可求得VP-ADC:VP-ABCD=1:2
所以V P-ANC:VP-ABCD=1-
 -
- =
=
故答案为:1:4
点评:本题考查空间几何体的体积度量、间接法解决问题.化不规则几何体为规则几何体,化不熟悉为熟悉间接求解,也是解决空间几何体体积的重要方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
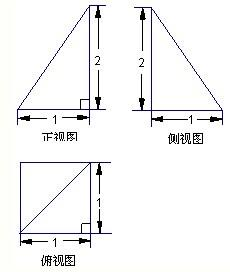 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
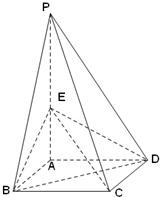 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: