题目内容
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C：
，过点P（-2，-4）的直线
的参数方程为
（t为参数）与C分别交于M，N.
（1）写出C的平面直角坐标系方程和的普通方程；
（2）若
，
，
成等比数列，求a 的值.
（1）
，
；（2）1.
【解析】
试题分析：（1）由
，在等式两边分别乘以
，再根据
.即可得C的直角坐标系方程；消去t即可得到直线
的方程.
（2）直线的参数方程与圆的方程联立，根据参数t的几何意义，以及
，
，
成等比数列，再结合韦达定理，可解出a的值.
试题解析：（1）曲线C的直角坐标方程为；
直线的普通方程为
.
（2）将直线1的参数方程与C的直角坐标方程联立，得
.
设点M，N分别对应参数t1，t2，恰为上述方程的根.
则
，
，
.
由题设得
，即
.
由（*）得
，
，则有
，得
，或
.
因为
，所以
.
考点：1.参数方程与普通方程互化.2.极坐标方程与直角坐标方程互化.3.直线与抛物线位置关系.
考点分析： 考点1：参数方程 试题属性- 题型：
- 难度：
- 考核：
- 年级：
练习册系列答案
相关题目
,其中
为自然对数的底数.
时，求曲线
在点
处的切线方程；
是
的导函数，求函数
在区间
上的最小值．
,
,△ABC的面积为
,则
=（ ）
B. 
C.
D.
时，函数
等于函数
的导函数，若输入函数
，则输出的函数
B.
D.
在不等式组
表示的平面区域上运动，则
的取值范围是（ ）
B.
C.
D.
.
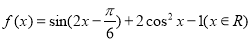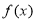的单调递增区间；
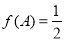，b，a，c成等差数列，且
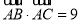，求a的值.
上有两个动点P，Q，E（3,0）为定点，EP⊥EQ，则
最小值为（ ）
C. 9 D. 
（本小题满分12分）
为了研究某种细菌在特定环境下，随时间变化繁殖情况，得如下实验数据：
天数t（天） | 3 | 4 | 5 | 6 | 7 |
繁殖个数y（千个） | 2.5 | 3 | 4 | 4.5 | 6 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测
时，细菌繁殖个数.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
.
，集合
，则
（ ）
