题目内容
19.已知函数f(x)=|x-a|+|x-2|,x∈R(Ⅰ)若关于x的不等式f(x)≤a在R上有解,求实数a的最小值M;
(Ⅱ)在(Ⅰ)的条件下,已知正实数m,n,p满足m+2n+3p=M,求$\frac{3}{m}$+$\frac{2}{n}$+$\frac{1}{p}$的最小值.
分析 (Ⅰ)关于x的不等式f(x)≤a在R上有解,求出f(x)的最小值,即可求实数a的最小值M;
(Ⅱ)利用柯西不等式,即可求$\frac{3}{m}$+$\frac{2}{n}$+$\frac{1}{p}$的最小值.
解答 解:(Ⅰ)f(x)=|x-a|+|x-2|≥|a-2|,
∵关于x的不等式f(x)≤a在R上有解,
∴|a-2|≤a,∴a≥1,
∴实数a的最小值M=1;
(Ⅱ)m+2n+3p=1,$\frac{3}{m}$+$\frac{2}{n}$+$\frac{1}{p}$=($\frac{3}{m}$+$\frac{2}{n}$+$\frac{1}{p}$)(m+2n+3p)≥($\sqrt{3}$+2+$\sqrt{3}$)2=16+8$\sqrt{3}$,
∴$\frac{3}{m}$+$\frac{2}{n}$+$\frac{1}{p}$的最小值为16+8$\sqrt{3}$.
点评 本题考查绝对值不等式的运用,考查柯西不等式在最值中的应用,考查计算能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
11.(1-2x)(1-x)5的展开式中x3的系数为( )
| A. | 10 | B. | -10 | C. | -20 | D. | -30 |
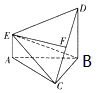 如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.
如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点. 已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )
已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )