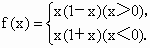题目内容
判断下列函数是否具有奇偶性.(1)f(x)=x3;
(2)f(x)=2x4+3x2;
(3)f(x)=x3+![]() ;
;
(4)f(x)=x+1.
思路解析:判断函数是奇函数或是偶函数按定义证明即可,同时还要注意:在公共定义域内,
(1)两个偶函数之和为偶函数,两个偶函数之积为偶函数;
(2)两个奇函数之和为奇函数,两个奇函数之积为偶函数;
(3)一个奇函数与一个偶函数之积为奇函数.
解:(1)f(-x)=(-x)3=-f(x),所以f(x)是奇函数.
(2)f(-x)=2(-x)4+3(-x)2=2x4+3x2=f(x),所以f(x)是偶函数.
(3)f(-x)=(-x)3+ -(x3+
-(x3+![]() )=-f(x),所以f(x)是奇函数.
)=-f(x),所以f(x)是奇函数.
(4)f(x)=x+1中,既没有f(-x)=f(x),也没有f(-x)=-f(x),所以f(x)为非奇非偶函数.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
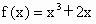 ;(2)
;(2)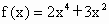 ;
;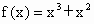 ;(4)f(x)=0.
;(4)f(x)=0. ;
;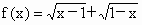 ;
;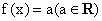 ;
;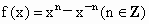 ;
;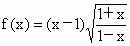 ;
;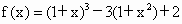 ;
;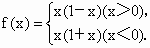
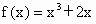 ;(2)
;(2) ;
;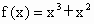 ;(4)f(x)=0.
;(4)f(x)=0.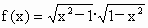 ;
;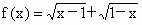 ;
;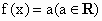 ;
;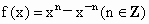 ;
; ;
; ;
;