题目内容
判断下列函数是否具有奇偶性.
(1)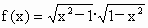 ;
;
(2)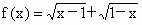 ;
;
(3)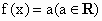 ;
;
(4)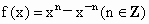 ;
;
(5)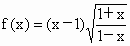 ;
;
(6) ;
;
(7)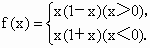
答案:略
解析:
解析:
|
解: (1)定义域{-1,1},此时f(x)=0,∴ f(x)既是奇函数又是偶函数.(2)∵定义域为{1},∴f(x)为非奇非偶函数. (3)a=0时,f(x)既是奇函数又是偶函数; a¹ 0时,f(x)为偶函数. (4)n=0时,f(x)既是奇函数又是偶函数; n为偶函数且n¹ 0时,f(x)是偶函数; n为奇数时,f(x)是奇函数. (5)函数的定义域为[-1,1), 故f(x)是非奇非偶函数. (6)函数的定义域为R,
故f(x)是奇函数. (7)定义域为{xÎ R|x¹ 0}, 而当x>0时,-x<0, f(-x)=-x(1-x)=-f(x); 当x<0时,-x>0,f(-x)=-x(1+x)=-f(x); ∴f(-x)=-f(x).故f(x)是奇函数. |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,
, .
.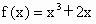 ;(2)
;(2)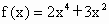 ;
;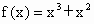 ;(4)f(x)=0.
;(4)f(x)=0. ;
;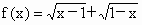 ;
;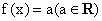 ;
;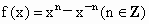 ;
;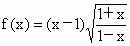 ;
;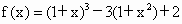 ;
;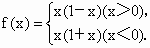
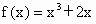 ;(2)
;(2) ;
;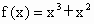 ;(4)f(x)=0.
;(4)f(x)=0.