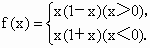题目内容
判断下列函数是否具有奇偶性.
(1)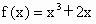 ;(2)
;(2)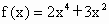 ;
;
(3)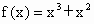 ;(4)f(x)=0.
;(4)f(x)=0.
答案:略
解析:
提示:
解析:
|
解: (1)函数的定义域为R,它关于坐标原点对称,又   . .
即 f(-x)=-f(x),所以函数  的奇函数. 的奇函数.
(2)函数的定义域是R,又 (3)函数的定义域为R,它关于原点对称, 但 所以 (4)函数的定义域为R,它关于原点对称, 因为f(-x)=0,f(x)=0, 即f(-x)=f(x),f(-x)=-f(x)同时成立. 所以f(x)=0既是奇函数又是偶函数. |
提示:
|
在判断一个函数的奇偶性时,首先要求定义域,否则判断会出现错误.如函数  ,若直接计算f(x)可满足f(-x)=-f(x),表面上看,好像是奇函数,但当x=1时,原函数无意义,x=-1时,原函数有意义,即f(-1)¹
-f(1),所以此函数为非奇非偶函数. ,若直接计算f(x)可满足f(-x)=-f(x),表面上看,好像是奇函数,但当x=1时,原函数无意义,x=-1时,原函数有意义,即f(-1)¹
-f(1),所以此函数为非奇非偶函数.
判断函数的奇偶性,包括判断一个函数是奇函数,或者是偶函数,或者不是奇函数也不是偶函数,或者既是奇函数又是偶函数. |

练习册系列答案
相关题目
 ,即f(-x)=f(x),所以函数
,即f(-x)=f(x),所以函数 是偶函数.
是偶函数. 与-f(x)和f(x)都不相等,
与-f(x)和f(x)都不相等, 为非奇非偶函数.
为非奇非偶函数. ;
;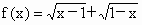 ;
;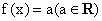 ;
;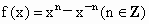 ;
;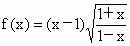 ;
;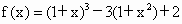 ;
;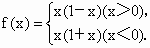
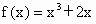 ;(2)
;(2) ;
;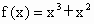 ;(4)f(x)=0.
;(4)f(x)=0.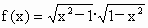 ;
;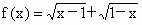 ;
;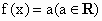 ;
;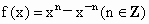 ;
;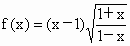 ;
; ;
;