题目内容
【题目】给出下列叙述:
①正四面体![]() 的棱长为
的棱长为![]() ,
,![]() 是棱
是棱![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值是
所成角的余弦值是![]() ;
;
②在等比数列![]() 中前
中前![]() 项和为
项和为![]() ,前
,前![]() 项和为
项和为![]() ,则前
,则前![]() 项和为
项和为![]() ;
;
③直线![]() 关于直线
关于直线![]() 对称的直线方程为
对称的直线方程为![]() ;
;
④若![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
其中所有正确叙述的序号是_____________.
【答案】①③④
【解析】
由异面直线所成角的定义可判断①;由等比数列的性质:当公比不为![]() ,由
,由![]() 成等比数列,计算可判断②;由直线关于直线对称的求法可判断③;由乘“1”法和基本不等式的运用可判断④
成等比数列,计算可判断②;由直线关于直线对称的求法可判断③;由乘“1”法和基本不等式的运用可判断④
①,正四面体OABC的棱长为1,D是棱OA的中点,取OC的中点H,连接DH,

由![]() ,可得∠BDH(或补角)为异面直线BD与AC所成角,
,可得∠BDH(或补角)为异面直线BD与AC所成角,
由![]() ,
,
则异面直线BD与AC所成角的余弦值是![]() ,故①正确;
,故①正确;
②,在等比数列![]() 中,前m项和为30,前2m项和为100,则公比不为-1,
中,前m项和为30,前2m项和为100,则公比不为-1,
由![]() 成等比数列,
成等比数列,
可得![]() 成等比数列,
成等比数列,
则![]() ,解得前3m项和为
,解得前3m项和为![]() ,故②错误;
,故②错误;
③直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,在直线
,在直线![]() 上取点
上取点![]() ,关于直线
,关于直线![]() 的对称点为
的对称点为![]()
则 解得
解得
可得对称直线方差为![]()
即![]() ,故③正确;
,故③正确;
④若![]() ,且
,且![]() ,即
,即![]()
则![]()
![]()
![]()
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,故④正确;
,故④正确;
故答案为:①③④

 口算能手系列答案
口算能手系列答案【题目】临近开学季,某大学城附近的一款“网红”书包销售火爆,其成本是每件15元.经多数商家销售经验,这款书包在未来1个月(按30天计算)的日销售量![]() (个)与时间
(个)与时间![]() (天)的关系如下表所示:
(天)的关系如下表所示:
时间( | 1 | 4 | 7 | 11 | 28 | … |
日销售量( | 196 | 184 | 172 | 156 | 88 | … |
未来1个月内,前15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数),后15天每天的价格
为整数),后15天每天的价格![]() (元/个)与时间
(元/个)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() (且
(且![]() 为整数).
为整数).
(1)认真分析表格中的数据,用所学过的一次函数、反比例函数的知识确定一个满足这些数据![]() (个)与
(个)与![]() (天)的关系式;
(天)的关系式;
(2)试预测未来1个月中哪一天的日销售利润最大,最大利润是多少?
(3)在实际销售的第1周(7天),商家决定每销售1件商品就捐赠![]() 元利润
元利润![]() 给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间
给该城区养老院.商家通过销售记录发现,这周中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
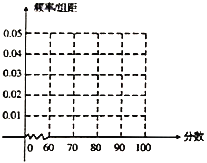
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.