题目内容
三棱柱 中,侧棱
中,侧棱
 平面
平面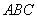 ,
,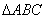 为等腰直角三角形,
为等腰直角三角形, 且
且 ,
, ,
, ,
, 分别是
分别是 ,
, ,
, 的中点.
的中点.
 (1)求证:
(1)求证: 平面
平面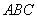 ;
;
(2)求证: 平面
平面 .
.
(1)(1)证明 取AB中点O,连接CO,DO,
∵DO∥AA1,DO= AA1,∴DO∥CE,DO=CE,
AA1,∴DO∥CE,DO=CE,
∴四边形DOCE为平行四边形,∴DE∥CO,DE⊄平面ABC,CO⊂平面ABC,
∴DE∥平面ABC. ……………5分
(2)证明 等腰直角三角形△ABC中F为斜边的中点,连接AF,∴AF⊥BC. ………6分
又∵三棱柱ABC-A1B1C1为直三棱柱,∴平面ABC⊥平面BB1C1C,
∴AF⊥平面BB1C1C,∴AF⊥B1F, …………8分
设AB=AA1=1,∴B1F= ,EF=
,EF= ,B1E=
,B1E= ,
,
∴B1F2+EF2=B1E2,∴B1F⊥EF,又AF∩EF=F,∴B1F⊥平面AEF. ………12分

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
为选拔选手参加“中国汉字听写大会”,举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为 )进行统计.按照
)进行统计.按照 ,
, ,
, ,
, ,
, 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
, 的数据).
的数据).
 |

(1)求样本容量 和频率分布直
和频率分布直 方图中的
方图中的 、
、 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机 抽取3名学生参加“中国汉字听写大会”,设随机变量
抽取3名学生参加“中国汉字听写大会”,设随机变量 表示所抽取的3名学生中得
表示所抽取的3名学生中得 分在
分在 内的学生人数,求随机变量
内的学生人数,求随机变量 的分布列及数学期望.
的分布列及数学期望.
 A.
A.



 则
则 的最大值为 .
的最大值为 . B.
B.
 D.
D.
 是真命题,
是真命题, 是假命题,则
是假命题,则 是真命题 (B)
是真命题 (B) 是假命题
是假命题  是真命题 (D)
是真命题 (D) 是真命题
是真命题 中,前四项之和为20,最后四项之和为60,前
中,前四项之和为20,最后四项之和为60,前 项之和是100,则项数
项之和是100,则项数 ”是“函数
”是“函数 上是增函数”的
上是增函数”的