题目内容
已知m∈{z|-1<z<1,z≠0},设p:y=mx+2 004的值随x的增大而增大;q:不等式x+|x-2m|>1的解集为R.当p、q有且只有一个正确时,求实数m的取值范围.思路分析:本题是函数、不等式与命题的综合题,涉及到函数的单调性和把不等式转化成求函数的最小值的问题,要解此题可以先分q和p正确与否,然后求出m的范围.
解:首先研究q,∵x+|x-2m|=∴x+|x-2m|的最小值是2m.
又∵不等式x+|x-2m|>1的解集为R,
∴2m>1,
∴m>![]() .
.
结合m∈{z|-1<z<1,z≠0}知,q正确时,![]() <m<1;q不正确时,-1<m≤
<m<1;q不正确时,-1<m≤![]() 且m≠0.
且m≠0.
其次研究p,y=mx+2 004的值随x的增大而增大,m>0,反之m≤0.
所以p正确时0<m<1,p不正确时-1<m<0.
综上可知,当p正确q不正确时,0<m≤![]() .
.
当p不正确q正确时,m∈![]() .
.
所以m的取值范围是{m|0<m≤![]() }.
}.
方法归纳 解答这类问题时要尽量把命题简化,再根据题设条件,推出所有可能的情况.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
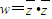 ,|w|=2|z|.
,|w|=2|z|.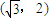 ,试求点P的坐标;
,试求点P的坐标;
 ,|w|=2|z|.
,|w|=2|z|.