题目内容
已知复数z=1-mi(m>0),z=x+yi和w=x'+y'i,其中x,y,x',y'均为实数,i为虚数单位,且对于任意复数z,有w=
 ,|w|=2|z|.
,|w|=2|z|.(Ⅰ)试求m的值,并分别写出x'和y'用x、y表示的关系式;
(Ⅱ)将(x、y)作为点P的坐标,(x'、y')作为点Q的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点P变到这一平面上的点Q,当点P在直线y=x+1上移动时,试求点P经该变换后得到的点Q的轨迹方程;
(Ⅲ)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由.
【答案】分析:(Ⅰ)由题设, ,求出|z|=2,继而求出m,再根据复数相等得出x'和y'用x、y表示的关系式;
,求出|z|=2,继而求出m,再根据复数相等得出x'和y'用x、y表示的关系式;
(Ⅱ)利用转换,代换的方法,求轨迹方程;
(Ⅲ)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,所求直线可设为y=kx+b(k≠0)
结合以上两问求解.
解答:解:(Ⅰ)由题设, ,∴|z|=2,
,∴|z|=2,
于是由 ,…(3分)
,…(3分)
因此由 ,
,
得关系式 …(5分)
…(5分)
(Ⅱ)设点P(x,y)在直线y=x+1上,则其经变换后的点Q(x',y')满足 ,…(7分)
,…(7分)
消去x,得 ,
,
故点Q的轨迹方程为 …(10分)
…(10分)
(3)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,
∴所求直线可设为y=kx+b(k≠0),…(12分)
[解法一]∵该直线上的任一点P(x,y),其经变换后得到的点 仍在该直线上,
仍在该直线上,
∴ ,
,
即 ,
,
当b≠0时,方程组 无解,
无解,
故这样的直线不存在. …(16分)
当b=0时,由 ,
,
得 ,
,
解得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,…(18分)
,…(18分)
[解法二]取直线上一点 ,其经变换后的点
,其经变换后的点 仍在该直线上,
仍在该直线上,
∴ ,
,
得b=0,…(14分)
故所求直线为y=kx,取直线上一点P(0,k),其经变换后得到的点 仍在该直线上.
仍在该直线上.
∴ ,…(16分)
,…(16分)
即 ,得
,得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,…(18分)
,…(18分)
点评:本题考查复数的有关概念和计算,轨迹方程的求解,考查转化、代入、计算、推理能力.
 ,求出|z|=2,继而求出m,再根据复数相等得出x'和y'用x、y表示的关系式;
,求出|z|=2,继而求出m,再根据复数相等得出x'和y'用x、y表示的关系式;(Ⅱ)利用转换,代换的方法,求轨迹方程;
(Ⅲ)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,所求直线可设为y=kx+b(k≠0)
结合以上两问求解.
解答:解:(Ⅰ)由题设,
 ,∴|z|=2,
,∴|z|=2,于是由
 ,…(3分)
,…(3分)因此由
 ,
,得关系式
 …(5分)
…(5分)(Ⅱ)设点P(x,y)在直线y=x+1上,则其经变换后的点Q(x',y')满足
 ,…(7分)
,…(7分)消去x,得
 ,
,故点Q的轨迹方程为
 …(10分)
…(10分)(3)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,
∴所求直线可设为y=kx+b(k≠0),…(12分)
[解法一]∵该直线上的任一点P(x,y),其经变换后得到的点
 仍在该直线上,
仍在该直线上,∴
 ,
,即
 ,
,当b≠0时,方程组
 无解,
无解,故这样的直线不存在. …(16分)
当b=0时,由
 ,
,得
 ,
,解得
 或
或 ,
,故这样的直线存在,其方程为
 或
或 ,…(18分)
,…(18分)[解法二]取直线上一点
 ,其经变换后的点
,其经变换后的点 仍在该直线上,
仍在该直线上,∴
 ,
,得b=0,…(14分)
故所求直线为y=kx,取直线上一点P(0,k),其经变换后得到的点
 仍在该直线上.
仍在该直线上.∴
 ,…(16分)
,…(16分)即
 ,得
,得 或
或 ,
,故这样的直线存在,其方程为
 或
或 ,…(18分)
,…(18分)点评:本题考查复数的有关概念和计算,轨迹方程的求解,考查转化、代入、计算、推理能力.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
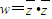 ,|w|=2|z|.
,|w|=2|z|.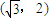 ,试求点P的坐标;
,试求点P的坐标;