题目内容
已知数列{an},Sn是其前n项和,且an=7Sn-1+2(n≥2),a1=2.(1)求数列{an} 的通项公式;
(2)设bn=
| 1 | log2an•log2an+1 |
分析:(1)根据n≥2,an=Sn-Sn-1,可得到数列{an} 的递推关系式,再化简,判断数列{an} 是等比数列,利用等比数列的通项公式求处即可.
(2)先根据(1)中求出的数列{an} 的通项公式,求出数列 {bn}的通项公式,再利用裂项相消法,求出数列 {bn}的前n项和,把n=10代入,即可得到T10的值.
(2)先根据(1)中求出的数列{an} 的通项公式,求出数列 {bn}的通项公式,再利用裂项相消法,求出数列 {bn}的前n项和,把n=10代入,即可得到T10的值.
解答:解:(1)∵n≥2时,an=7Sn-1+2,∴an+1=7Sn+2,an+1-an=7an,
∴an+1=8an,(n≥2)
又a1=2.∴a2=16=8a1.
an+1=8an,(n≥N*)
∴数列{an}是一个以2为首项,8为公比的等比数列
∴数列an=23n-2
(2)bn=
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)∴T10=
∴an+1=8an,(n≥2)
又a1=2.∴a2=16=8a1.
an+1=8an,(n≥N*)
∴数列{an}是一个以2为首项,8为公比的等比数列
∴数列an=23n-2
(2)bn=
| 1 |
| log2an•log2an+1 |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
∴Tn=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 10 |
| 31 |
点评:本题主要考查了递推公式求通项公式,以及裂项相消求和的应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
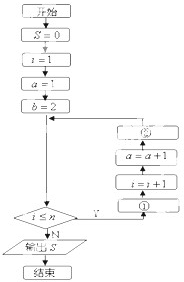 已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.
已知数列{an}的通项公式为an=n•2n,为了求数列{an}的和,现已给出该问题的算法程序框图.