题目内容
已知焦点在
轴上的椭圆的离心率为
，它的长轴长等于圆
的半径，则椭圆的标准方程是（ ）
A． | B． | C． | D． |
D
解析试题分析：圆的方程化成标准形式为：
所以
因为离心率
所以
又因为椭圆焦点在轴上，所以椭圆的标准方程为：.
考点：本小题主要考查椭圆标准方程的求法和圆的方程的认识，考查学生的运算求解能力.
点评：求椭圆的标准方程，应该知道焦点在哪个坐标轴上，再求标准方程中的基本量，其中往往少不了离心率的计算.
练习册系列答案
名校课堂系列答案
相关题目
已知圆
的圆心为抛物线
的焦点,且与直线
相切,则该圆的方程为( )
A． | B． |
C． | D． |
将圆
平分的直线是( )
A． | B． | C． | D． |
若圆
关于直线
对称，则直线的斜率是( )
| A．6 | B． | C． | D． |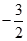
若双曲线
的一个焦点是圆
的圆心，且虚轴长为
，则双曲线的离心率为
A． | B． |
C． | D． |
已知圆的方程为
.设该圆过点（3，5）的两条弦分别为AC和BD，且
.则四边形ABCD的面积最大值为（ ）
A．20 | B．30 | C．49 | D．50 |
自点A（3，5）作圆C：
的切线，求切线的方程（ ）
A． | B． |
| C．或 | D．以上都不对 |
方程
表示的图形是（ ）
A．以 为圆心， 为半径的圆 |
B．以 为圆心，为半径的圆 |
C．以 为圆心，为半径的圆 |
D．以 为圆心，为半径的圆 |
已知直线
与圆
相交于
、
两点，若
，则实数
的值为（ ）
A． | B． 或 | C． | D． |