题目内容
设函数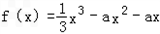 ,g(x)=2x2+4x+c.
,g(x)=2x2+4x+c.
(1)试问函数f(x)能否在x=﹣1时取得极值?说明理由;
(2)若a=﹣1,当x∈[﹣3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
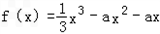 ,g(x)=2x2+4x+c.
,g(x)=2x2+4x+c.(1)试问函数f(x)能否在x=﹣1时取得极值?说明理由;
(2)若a=﹣1,当x∈[﹣3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
解:(1)由题意f'(x)=x2﹣2ax﹣a, 假设在x=﹣1时f(x)取得极值,则有f'(﹣1)=1+2a﹣a=0,
∴a=﹣1, 而此时,f'(x)=x2+2x+1=(x+1)2≥0,函数f(x)在R上为增函数,无极值.
这与f(x)在x=﹣1有极值矛盾,所以f(x)在x=﹣1处无极值;
(2)令f(x)=g(x),则有 x3﹣x2﹣3x﹣c=0,
x3﹣x2﹣3x﹣c=0,
∴c= x3﹣x2﹣3x,
x3﹣x2﹣3x,
设F(x)= x3﹣x2﹣3x,G(x)=c,
x3﹣x2﹣3x,G(x)=c,
令F'(x)=x2﹣2x﹣3=0,
解得x=﹣1或x=3.
列表如下:
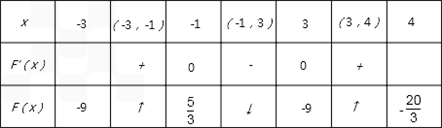
由此可知:F(x)在(﹣3,﹣1)、(3,4)上是增函数,在(﹣1,3)上是减函数.
当x=﹣1时,F(x)取得极大值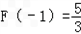 ;
;
当x=3时,F(x)取得极小值F(﹣3)=F(3)=﹣9,而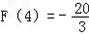 .
.
如果函数f(x)与g(x)的图象有两个公共点,则函数F(x)与G(x)有两个公共点,
所以,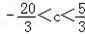 或c=﹣9.
或c=﹣9.
∴a=﹣1, 而此时,f'(x)=x2+2x+1=(x+1)2≥0,函数f(x)在R上为增函数,无极值.
这与f(x)在x=﹣1有极值矛盾,所以f(x)在x=﹣1处无极值;
(2)令f(x)=g(x),则有
 x3﹣x2﹣3x﹣c=0,
x3﹣x2﹣3x﹣c=0,∴c=
 x3﹣x2﹣3x,
x3﹣x2﹣3x,设F(x)=
 x3﹣x2﹣3x,G(x)=c,
x3﹣x2﹣3x,G(x)=c,令F'(x)=x2﹣2x﹣3=0,
解得x=﹣1或x=3.
列表如下:

由此可知:F(x)在(﹣3,﹣1)、(3,4)上是增函数,在(﹣1,3)上是减函数.
当x=﹣1时,F(x)取得极大值
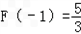 ;
;当x=3时,F(x)取得极小值F(﹣3)=F(3)=﹣9,而
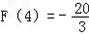 .
.如果函数f(x)与g(x)的图象有两个公共点,则函数F(x)与G(x)有两个公共点,
所以,
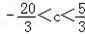 或c=﹣9.
或c=﹣9.
练习册系列答案
相关题目