题目内容
(本小题12分)若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足
分别满足![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1) 判断函数![]() 的零点个数并证明你的结论;
的零点个数并证明你的结论;
(2) 函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
(12分)(1) 函数![]() 只有一个零点。
只有一个零点。
证明![]()
![]() ,
, ![]() .
.
当![]() 时,
时,![]() .
.![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;∴当
递增;∴当![]() 时,
时,![]() 取极小值,其极小值为
取极小值,其极小值为![]() .
.
所以函数![]() 只有一个零点。
只有一个零点。
(2)解法一:由(1)可知函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,
处有公共点,
因此若存在![]() 和
和![]() 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点.
设隔离直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() 当
当![]() 时恒成立
时恒成立
![]() ,
, ![]() 由
由![]() ,得
,得![]() .
.
下面证明![]() 当
当![]() 时恒成立.令
时恒成立.令![]()
![]() ,
,
则![]() , 当
, 当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;当
递增;当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;∴当
递减;∴当![]() 时,
时,![]() 取极大值,其极大值为
取极大值,其极大值为![]() .
.
从而![]() ,即
,即![]() 恒成立.
恒成立.
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() .
.
解法二: 由(1)可知当![]() 时,
时,![]() (当且当
(当且当![]() 时取等号) .
时取等号) .
若存在![]() 和
和![]() 的隔离直线,则存在实常数
的隔离直线,则存在实常数![]() 和
和![]() ,
,
使得![]() 和
和![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 且
且![]()
![]() ,即
,即![]() .后面解题步骤同解法一.
.后面解题步骤同解法一.

练习册系列答案
相关题目
 )的直线l过点(0,-2
)的直线l过点(0,-2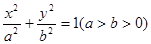
 cot∠MON
≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON
≠0(O为原点).若存在,求直线m的方程;若不存
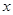 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为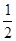 ,且经过点
,且经过点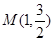 ,过点P(2,1)的直线
,过点P(2,1)的直线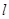 与椭圆C相交于不同的两点A、B.
与椭圆C相交于不同的两点A、B.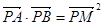 ?若存在,求出直线
?若存在,求出直线 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
 .
.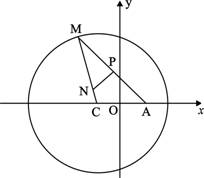 (本小题满分12分) 如图所示,已知圆
(本小题满分12分) 如图所示,已知圆