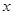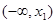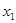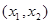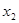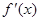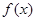题目内容
(本小题满分12分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围;
(II)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.
【答案】
解:(1)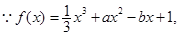
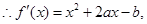 由题意
由题意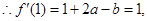
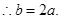 ①
①
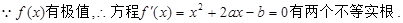
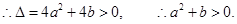 ②
②
由①、②可得,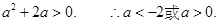
故实数a的取值范围是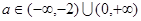 ………4分
………4分
(2)存在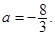
由(1)可知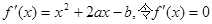 ,
,
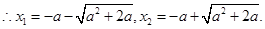
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
单调增 |
极大值 |
单调减 |
极小值 |
单调增 |
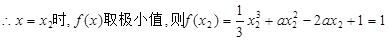 ,
,
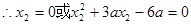 .
.
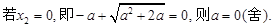

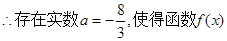 的极小值为1. ………8分
的极小值为1. ………8分
(3)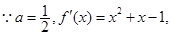
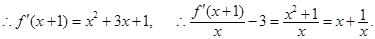
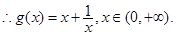

∴其中等号成立的条件为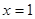 .
.
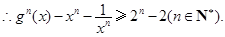 ………12分
………12分
另证:当n=1时,左=0,右=0,原不等式成立.
假设n=k (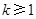 )时成立,即
)时成立,即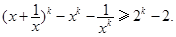
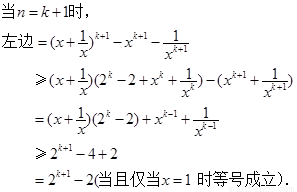
即当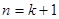 时原不等式成立.
时原不等式成立.
综上当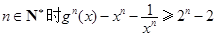 成立.
………12分
成立.
………12分
【解析】略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目