题目内容
Sn是数列{an}的前n项和,若Sn=2an-2(n∈N*),则数列{an}的通项公式为________.
an=2n,n∈N*
分析:当n=1时,a1=2,当n≥2时,由Sn=2an-2,Sn-1=2an-1-2,知Sn-Sn-1=2an-2an-1,从而得到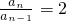 ,故{an}是首项为2,公比为2的等比数列.
,故{an}是首项为2,公比为2的等比数列.
解答:当n=1时,a1=S1=2a1-2,∴a1=2.
当n≥2时,Sn=2an-2,∴Sn-1=2an-1-2,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴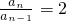 ,
,
∴{an}是首项为2,公比为2的等比数列,∴an=2n,n∈N*.
答案:an=2n,n∈N*.
点评:本题考查等比数列的通项公式的求法,解题时要熟练掌握等比数列的性质和应用.
分析:当n=1时,a1=2,当n≥2时,由Sn=2an-2,Sn-1=2an-1-2,知Sn-Sn-1=2an-2an-1,从而得到
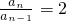 ,故{an}是首项为2,公比为2的等比数列.
,故{an}是首项为2,公比为2的等比数列.解答:当n=1时,a1=S1=2a1-2,∴a1=2.
当n≥2时,Sn=2an-2,∴Sn-1=2an-1-2,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴
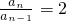 ,
,∴{an}是首项为2,公比为2的等比数列,∴an=2n,n∈N*.
答案:an=2n,n∈N*.
点评:本题考查等比数列的通项公式的求法,解题时要熟练掌握等比数列的性质和应用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目