题目内容
设x,y∈R,a>1,b>1,若ax=by=2,a+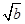 =4,则
=4,则 +
+ 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |
A
解析

练习册系列答案
相关题目
已知 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
下列各式中,最小值等于2的是( )
A. | B. | C. | D. |
下列结论正确的是 ( )
A.当 |
B. |
C. |
D. |
设正实数 满足
满足 ,则当
,则当 取得最大小值时,
取得最大小值时, 的最大值为( )
的最大值为( )
| A.0 | B.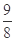 | C.2 | D. |
函数y= (x>-1)的图象最低点的坐标为( )
(x>-1)的图象最低点的坐标为( )
| A.(1,2) | B.(1,-2) | C.(1,1) | D.(0,2) |
已知a>0,b>0,且2a+b=4,则 的最小值为( )
的最小值为( )
A. | B.4 | C. | D.2 |
若a>b>0,则代数式a2+ 的最小值为( )
的最小值为( )
| A.2 | B.3 | C.4 | D.5 |
 的一元二次不等式
的一元二次不等式
 时,求不等式
时,求不等式 取什么值时,关于
取什么值时,关于