题目内容
如图,在直角三角形ABC中,![]() ,D为BC的中点,
,D为BC的中点,![]() ,
,![]() ,以A、B为焦点的椭圆经过点C。
,以A、B为焦点的椭圆经过点C。
(I)建立适当的直角坐标系,求椭圆的方程;
(II)是否存在不平行于AB的直线l与(I)中椭圆交于不同两点M、N,使![]() ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由。
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由。

解:(I)以AB所在的直线为x轴,AB的垂直平分线为y轴建立直角坐标系,则
![]() 。
。
设椭圆方程为![]() ,
,![]() ,于是
,于是 解得
解得 ,
,
![]() 所求椭圆方程为
所求椭圆方程为![]() 。
。
(II)![]() 条件
条件![]() 等价于
等价于![]()
![]() 若存在符合条件的直线,该直线的斜率一定存在,否则与点D(0,
若存在符合条件的直线,该直线的斜率一定存在,否则与点D(0,![]() )不在x轴上矛盾。
)不在x轴上矛盾。
![]() 可设直线l:
可设直线l:![]()
由 得
得![]()
由![]() 得
得![]() 。
。
设![]() 的中点为Q
的中点为Q![]() ,
,
则![]() 。
。
 ,即
,即 。
。
解得:![]()
(将点的坐标代入![]() 亦可得到此结果)
亦可得到此结果)
由![]() ,
,![]() 得
得![]()
![]()
![]() 存在满足条件的直线
存在满足条件的直线![]() ,其斜率的取值范围是
,其斜率的取值范围是![]() 。
。

练习册系列答案
相关题目
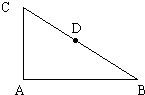 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,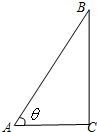 如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
如图,在直角三角形ABC中,斜边AB=4.设角A=θ,△ABC的面积为S
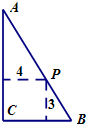 (2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )
(2012•贵州模拟)如图,在直角三角形ABC的斜边AB上有一点P,它到这个三角形两条直角边的距离分别为4和3,则△ABC面积的最小值是( )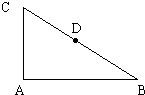 如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,
如图,在直角三角形ABC中,∠BAC=90°,D为BC的中点,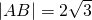 ,
,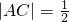 ,以A、B为焦点的椭圆经过点C.
,以A、B为焦点的椭圆经过点C.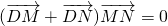 ?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.
?若存在,求出直线l斜率的取值范围;若不存在,请说明理由.