题目内容
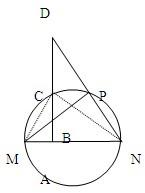 12、已知:如图,MN为圆的直径,P、C为圆上两点,连PM、PN,过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D,求证:AC2=AB•AD.
12、已知:如图,MN为圆的直径,P、C为圆上两点,连PM、PN,过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D,求证:AC2=AB•AD.分析:首先用两个角对应相等证明两个三角形相似,在相似三角形中写出对应边成比例,又根据直角三角形的射影定理,得到比例式,结合两个比例式,得到要证明的结论.
解答:证明:在△ABM与△AND中,
∠BAM=∠NAD=90°
∠AMB=∠ADN=90-∠MND,
∴△ABM∽△AND,
AB:AN=AM:AD,
AN•AM=AB•AD①
又∵在直角△MCN中,AC⊥MN,
∴AC2=AM•AN②
由①,②得AC2=AB•AD.
∠BAM=∠NAD=90°
∠AMB=∠ADN=90-∠MND,
∴△ABM∽△AND,
AB:AN=AM:AD,
AN•AM=AB•AD①
又∵在直角△MCN中,AC⊥MN,
∴AC2=AM•AN②
由①,②得AC2=AB•AD.
点评:本题考查相似三角形的证明和性质,考查直角三角形的射影定理,是一个证明对应线段成比例的问题,是一个基础题.

练习册系列答案
相关题目
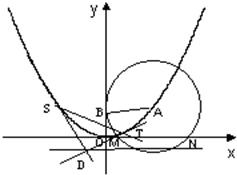 如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.
如图,已知圆A过定点B(0,2),圆心A在抛物线C:x2=4y上运动,MN为圆A在x轴上所截得的弦.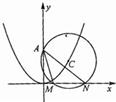 已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦.
已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦. 已知:如图,MN为圆的直径,P、C为圆上两点,连PM、PN,过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D,求证:AC2=AB•AD.
已知:如图,MN为圆的直径,P、C为圆上两点,连PM、PN,过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D,求证:AC2=AB•AD.