题目内容

已知向量
a
=
e1
-
e2
，
b
=4
e1
+3
e2
，其中
e1
=(1，0)，
e2
=(0，1)．
（1）试计算
a
•
b
及|  
a
+
b
|的值；
（2）求向量
a
与
b
的夹角的大小．
分析：（1）先由条件求得可得
a
=(1，-1)，
b
=(4 ，3)，利用两个向量的数量积公式求出
a
•
b
的值，再利用向量的模的定义求出|
a
+
b
|．
（2）设
a
与
b
的夹角为θ，则由两个向量夹角公式cosθ=
a
•
b
|
a
|•|
b
|
 求出cosθ的值，再由θ∈[0，π]，求出θ 的值．
解答：解：（1）由已知
a
=
e1
-
e2
，
b
=4
e1
+3
e2
，其中
e1
=(1，0)，
e2
=(0，1)，可得
a
=(1，-1)，
b
=(4 ，3)．
∴
a
•
b
=1×4+（-1）×3=1．
∵
a
+
b
=（5，2），∴| 
a
+
b
|=
25+4
=
29
．
（2）设
a
与
b
的夹角为θ，则 cosθ=
a
•
b
|
a
|•|
b
|
=
1
2
×5
=
2
10
．
又 θ∈[0，π]，∴θ=arccos
2
10
．
点评：本题主要考查两个向量的数量积的定义，数量积公式的应用，两个向量坐标形式的运算，两个向量夹角公式，根据三角函数的值求角，属于中档题．
练习册系列答案
相关题目
（1）选修4-2：矩阵与变换
已知二阶矩阵M有特征值λ=3及对应的一个特征向量
e1
=
1
1
，并且矩阵M对应的变换将点（-1，2）变换成（3，0），求矩阵M．
（2）选修4-4：坐标系与参数方程
过点M（3，4），倾斜角为
π
6
的直线l与圆C：
x=2+5cosθ
y=1+5sinθ
（θ为参数）相交于A、B两点，试确定|MA|•|MB|的值．
（3）选修4-5：不等式选讲
已知实数a，b，c，d，e满足a+b+c+d+e=8，a2+b2+c2+d2+e2=16，试确定e的最大值．
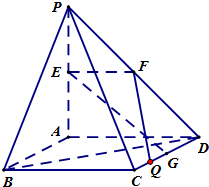精英家教网（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
（文）已知坐标平面内的一组基向量为
e
1=(1，sinx)，
e
2=(0，cosx)，其中x∈[0，
π
2
)，且向量
a
=
1
2
e
1+
3
2
e
2．
（1）当
e
1和
e
2都为单位向量时，求|
a
|；
（2）若向量
a
和向量
b
=(1，2)共线，求向量
e
1和
e
2的夹角．
已知A、B是椭圆的一条弦，向量与AB交于M，且，以M为焦点，以椭圆的右准线为相应的双曲线与直线AB交于N(4，-1)。

（1）求椭圆的离心率e；

（2）设双曲线的离心率为e2，e1+e2=f(a)，求f(a)的解析式，并求它的定义域和值域。
（1）选修4-2：矩阵与变换
已知二阶矩阵M有特征值λ=3及对应的一个特征向量
e1
=
1
1
，并且矩阵M对应的变换将点（-1，2）变换成（3，0），求矩阵M．
（2）选修4-4：坐标系与参数方程
过点M（3，4），倾斜角为
π
6
的直线l与圆C：
x=2+5cosθ
y=1+5sinθ
（θ为参数）相交于A、B两点，试确定|MA|•|MB|的值．
（3）选修4-5：不等式选讲
已知实数a，b，c，d，e满足a+b+c+d+e=8，a2+b2+c2+d2+e2=16，试确定e的最大值．
已知平面l上L的方向向量e=(-,),点O(0,0)和A(1,-2)在L上的射影分别是O1和A1,则=λe1,其中λ等于(    )

A.                B.-                   C.2                  D.-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网