题目内容
已知数列![]() 的首项
的首项![]() ,
,![]() .
.
(1)求证:数列 为等比数列;
为等比数列;
(2) 记![]() ,若
,若![]() ,求最大的正整数
,求最大的正整数![]() .
.
(3)是否存在互不相等的正整数![]() ,使
,使![]() 成等差数列且
成等差数列且![]() 成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
成等比数列,如果存在,请给出证明;如果不存在,请说明理由.
(1)∵![]() ,∴
,∴![]() ,…………………………………1分
,…………………………………1分
且∵![]() ,∴
,∴![]() , …………………………………………2分
, …………………………………………2分
∴数列 为等比数列. …………………………………………………………3分
为等比数列. …………………………………………………………3分
(2)由(1)可求得![]() ,∴
,∴![]() .…………………………4分
.…………………………4分
![]()
 ,……6分
,……6分
若![]() ,则
,则![]() ,∴
,∴![]() .………………………………………8分
.………………………………………8分
(3)假设存在,则![]() , ……………………………9分
, ……………………………9分
∵![]() ,∴
,∴![]() .………………………10分
.………………………10分
化简得:![]() ,……………………………………………………………11分
,……………………………………………………………11分
∵![]() ,当且仅当
,当且仅当![]() 时等号成立.………………………12分
时等号成立.………………………12分
又![]() 互不相等,∴不存在. ……………………………………………………13分
互不相等,∴不存在. ……………………………………………………13分

练习册系列答案
相关题目
已知数列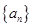 的首项
的首项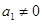 ,其前
,其前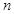 项的和为
项的和为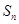 ,且
,且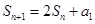 ,则
,则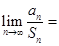
| A.0 | B.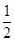 | C.1 | D.2 |
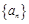 的首项为
的首项为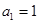 ,且
,且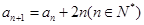 ,则这个数列的通项公式为___________
,则这个数列的通项公式为___________