题目内容
(本题满分14分,其中第1小题6分,第2小题8分)
已知数列![]() 的首项为1,前
的首项为1,前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) 当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
略
解析:
略(1) 由![]() … (1) , 得
… (1) , 得![]() … (2),由 (2)-(1) 得
… (2),由 (2)-(1) 得
![]() , 整理得
, 整理得 ![]() ,
,![]() .
.
所以,数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…是以4为公比的等比数列.
,…是以4为公比的等比数列.
其中,![]() ,
,
所以,![]() .
.
(2)由题意,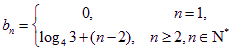 .
.
当![]() 时,
时,
![]()
![]()
![]()
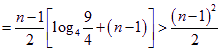
所以,![]() .
.
又当![]() 时,
时,![]() ,
,![]() .
.
故综上,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列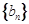 满足
满足 ,
, 为数列
为数列 、
、 和
和 ,不等式
,不等式 恒成立,求实数
恒成立,求实数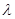 的取值范围
的取值范围 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,且
,且 .
. 求
求 的长
的长 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 ,
, 是它实轴的两个端点,
是它实轴的两个端点, 是其虚轴的一个端点.已知其一条渐近线的一个方向向量是
是其虚轴的一个端点.已知其一条渐近线的一个方向向量是 ,
, 的面积是
的面积是 ,
, 为坐标原点,直线
为坐标原点,直线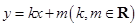 与双曲线C相交于
与双曲线C相交于 、
、 两点,且
两点,且 .
. 的方程;
的方程; 的轨迹方程,并指明是何种曲线.
的轨迹方程,并指明是何种曲线. 是等腰梯形,其中
是等腰梯形,其中 米,梯形的高为
米,梯形的高为 米,
米, 米,上部
米,上部 是个半圆,固定点
是个半圆,固定点 为
为 的中点.△
的中点.△ 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风), 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和 之间的距离为
之间的距离为 米,试将三角通风窗
米,试将三角通风窗 (平方米)表示成关于
(平方米)表示成关于 ;
;