题目内容
(2012•泰州二模)已知椭圆
+
=1(a>b>0)的右焦点为F1(2,0),离心率为e.
(1)若e=
,求椭圆的方程;
(2)设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,若原点O在以线段MN为直径的圆上.
①证明点A在定圆上;
②设直线AB的斜率为k,若k≥
,求e的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若e=
| ||
| 2 |
(2)设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,若原点O在以线段MN为直径的圆上.
①证明点A在定圆上;
②设直线AB的斜率为k,若k≥
| 3 |
分析:(1)利用离心率的计算公式e=
及b2=a2-c2即可得出椭圆的标准方程;
(2)利用①的结论,设出直线AB的方程与椭圆的方程联立即可得出关于a、b与k的关系式,再利用斜率与a、b的关系及其不等式的性质即可得出.
| c |
| a |
(2)利用①的结论,设出直线AB的方程与椭圆的方程联立即可得出关于a、b与k的关系式,再利用斜率与a、b的关系及其不等式的性质即可得出.
解答:解:(1)由e=
=
,c=2,得a=2
,b=
=2.
故所求椭圆方程为
+
=1.
(2)设A(x1,y1),则B(-x1,-y1),故M(
,
),N(
,-
).
①由题意,得
•
=0.化简,得
+
=4,∴点A在以原点为圆心,2为半径的圆上.
②设A(x1,y1),则
得到
+
=
(1+k2).
将e=
=
,b2=a2-c2=
-4,代入上式整理,得k2(2e2-1)=e4-2e2+1;
∵e4-2e2+1>0,k2>0,∴2e2-1>0,∴e>
.
∴k2=
≥3.化简,得
.解之,得
<e2≤4-2
,
<e≤
-1.
故离心率的取值范围是(
,
-1].
| ||
| 2 |
| c |
| a |
| 2 |
| a2-c2 |
故所求椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)设A(x1,y1),则B(-x1,-y1),故M(
| x1+2 |
| 2 |
| y1 |
| 2 |
| 2-x1 |
| 2 |
| y1 |
| 2 |
①由题意,得
| OM |
| ON |
| x | 2 1 |
| y | 2 1 |
②设A(x1,y1),则
|
| 1 |
| a2 |
| k2 |
| b2 |
| 1 |
| 4 |
将e=
| c |
| a |
| 2 |
| a |
| 4 |
| e2 |
∵e4-2e2+1>0,k2>0,∴2e2-1>0,∴e>
| ||
| 2 |
∴k2=
| e4-2e2+1 |
| 2e2-1 |
|
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
故离心率的取值范围是(
| ||
| 2 |
| 3 |
点评:熟练掌握椭圆的标准方程及其性质、参数a、b、c的关系、中点坐标公式、直线方程、离心率的计算公式、不等式的基本性质是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
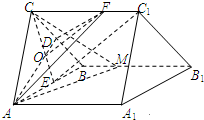 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.