题目内容
设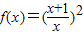 (x>0).
(x>0).(1)求f(x)的反函数f-1(x)
(2)若x≥2时,不等式
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(1)从条件中函数式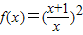 =y,(x>0)中反解出x,再将x,y互换即得f(x)的反函数f-1(x).
=y,(x>0)中反解出x,再将x,y互换即得f(x)的反函数f-1(x).
(2)利用(1)的结论,将不等式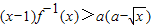 化成
化成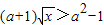 ,下面对a分类讨论:①当a+1>0;②当a+1<0.分别求出求实数a的取值范围,最后求它们的并集即可.
,下面对a分类讨论:①当a+1>0;②当a+1<0.分别求出求实数a的取值范围,最后求它们的并集即可.
解答:解:(1)∵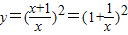 (x>0)∴y>1(2分)
(x>0)∴y>1(2分)
由原式有: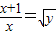 ∴
∴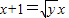
∴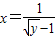 (2分)
(2分)
∴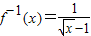 x∈(1,+∞)(2分)
x∈(1,+∞)(2分)
(2)∵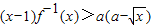
∴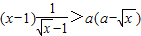 (x>0)
(x>0)
∴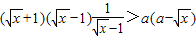
∴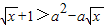
∴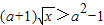 (2分)
(2分)
①当a+1>0即a>-1时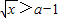 对x≥2恒成立
对x≥2恒成立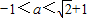
②当a+1<0即a<-1时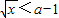 对x≥2恒成立
对x≥2恒成立
∴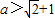 此时无解(3分)
此时无解(3分)
综上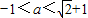 -(1分)
-(1分)
点评:本小题主要考查反函数、函数恒成立问题等基础知识,考查运算求解能力.求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).
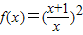 =y,(x>0)中反解出x,再将x,y互换即得f(x)的反函数f-1(x).
=y,(x>0)中反解出x,再将x,y互换即得f(x)的反函数f-1(x).(2)利用(1)的结论,将不等式
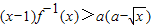 化成
化成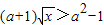 ,下面对a分类讨论:①当a+1>0;②当a+1<0.分别求出求实数a的取值范围,最后求它们的并集即可.
,下面对a分类讨论:①当a+1>0;②当a+1<0.分别求出求实数a的取值范围,最后求它们的并集即可.解答:解:(1)∵
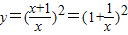 (x>0)∴y>1(2分)
(x>0)∴y>1(2分)由原式有:
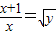 ∴
∴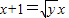
∴
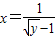 (2分)
(2分)∴
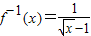 x∈(1,+∞)(2分)
x∈(1,+∞)(2分)(2)∵
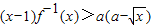
∴
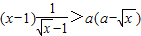 (x>0)
(x>0)∴
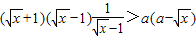
∴
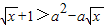
∴
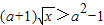 (2分)
(2分)①当a+1>0即a>-1时
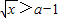 对x≥2恒成立
对x≥2恒成立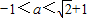
②当a+1<0即a<-1时
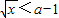 对x≥2恒成立
对x≥2恒成立∴
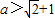 此时无解(3分)
此时无解(3分)综上
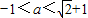 -(1分)
-(1分)点评:本小题主要考查反函数、函数恒成立问题等基础知识,考查运算求解能力.求反函数,一般应分以下步骤:(1)由已知解析式y=f(x)反求出x=Ф(y);(2)交换x=Ф(y)中x、y的位置;(3)求出反函数的定义域(一般可通过求原函数的值域的方法求反函数的定义域).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

 (x>0).
(x>0). 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.