题目内容
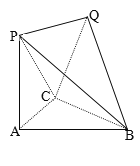
【题目】如图，在四棱锥P-ABCD中，
平面PCD，
，
，
，E为AD的中点，AC与BE相交于点O.
（1）证明：
平面ABCD.
（2）求直线BC与平面PBD所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）通过证明
平面
，得到
，再证
即可证得
平面ABCD.
（2）建立空间直角坐标系，求出平面的法向量、直线的方向向量，利用空间向量法求出线面角的正弦值.
（1）证明：
平面PCD，
平面
，
，
，
为
的中点，则
且
.
四边形BCDE为平行四边形，
，
.
又
，且E为AD的中点，四边形ABCE为正方形，
，又
平面，
平面，则.
平面
平面，
，
又
，
为等腰直角三角形，
O为斜边AC上的中点，
且
平面ABCD.
（2）解：以O为坐标原点，建立空间直角坐标系O-xyz，如图所示
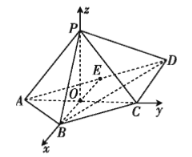
不妨设
，则
,
则
.
设平面PBD的法向量为
，
则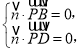
即
即
令
，得
.
设BC与平面
所成角为
，
则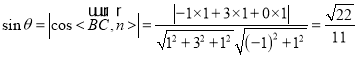
.
练习册系列答案
小学能力测试卷系列答案
相关题目
