题目内容
定义区间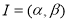 的长度为
的长度为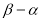 ,已知函数
,已知函数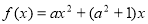 ,其中
,其中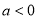 ,
,
区间 .
.
(1)求区间 的长度;
的长度;
(2)设区间 的长度函数为
的长度函数为 ,
, ,问:是否存在实数
,问:是否存在实数 ,使得
,使得
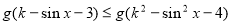 对一切
对一切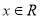 恒成立,若存在,求出
恒成立,若存在,求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
题目内容
定义区间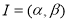 的长度为
的长度为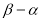 ,已知函数
,已知函数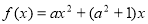 ,其中
,其中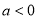 ,
,
区间 .
.
(1)求区间 的长度;
的长度;
(2)设区间 的长度函数为
的长度函数为 ,
, ,问:是否存在实数
,问:是否存在实数 ,使得
,使得
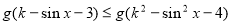 对一切
对一切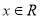 恒成立,若存在,求出
恒成立,若存在,求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案