题目内容
选修4-5:不等式选讲
已知 ,函数
,函数 的最小值为1.
的最小值为1.
(1)求 的值;
的值;
(2)求证: .
.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组
及频数分布表和频率分布直方图:
组号 | 分组 | 频数 |
1 |
| 12 |
2 |
| 16 |
3 |
| 34 |
4 |
| 44 |
5 |
| 50 |
6 |
| 24 |
7 |
| 12 |
8 |
| 4 |
9 |
| 4 |
合计 | 200 | |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的 的值;
的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球所占用时间的情况,采用分层抽样的方法,收集300位业余足球运动员每周平均踢足球所占用时间的样本数据(单位:小时),得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图(如图所示),其中样本数据的分组区间为: .将“业余运动员的每周平均踢足球所占用时间超过4小时”定义为“热爱足球”.
.将“业余运动员的每周平均踢足球所占用时间超过4小时”定义为“热爱足球”.
(1)应收集多少位女运动员的样本数据?
(2)估计该地区每周平均踢足球所占用时间超过4小时的概率;
(3)在样本数据中,有80位女运动员“热爱足球”,请画出“热爱足球与性别”列联表,并判断是否有99%的把握认为“热爱足球与性别”有关.

附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |


 ,则
,则 的值是
的值是 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 ”的否定是“
”的否定是“ ”
” 的方程
的方程 的两实根异号的充要条件是
的两实根异号的充要条件是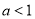
 是
是 上的偶函数,则
上的偶函数,则 的图象的对称轴是
的图象的对称轴是 .
. 是抛物线
是抛物线 的焦点,点
的焦点,点 为抛物线
为抛物线 的对称轴与其准线的交点,过
的对称轴与其准线的交点,过 ,若点
,若点 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( ) B.
B. C.
C. D.
D.
 :
: ,过
,过 轴上的点
轴上的点 向圆
向圆 引切线,则切线长为( )
引切线,则切线长为( ) B.
B. C.
C. D.
D.









 的左顶点和上顶点分别为
的左顶点和上顶点分别为 ,左、右焦点分别是
,左、右焦点分别是 ,在线段
,在线段 上有且只有一个点
上有且只有一个点 满足
满足 ,则椭圆的离心率的平方为( )
,则椭圆的离心率的平方为( ) B.
B. C.
C. D.
D.


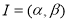 的长度为
的长度为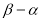 ,已知函数
,已知函数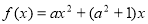 ,其中
,其中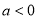 ,
, .
. 的长度;
的长度; ,
, ,问:是否存在实数
,问:是否存在实数 ,使得
,使得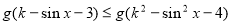 对一切
对一切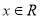 恒成立,若存在,求出
恒成立,若存在,求出 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.