题目内容
函数y=tan2x的定义域是
- A.{x|x≠
 +kπ,x∈R,k∈Z}
+kπ,x∈R,k∈Z} - B.{x|x≠
 +2kπ,x∈R,k∈Z}
+2kπ,x∈R,k∈Z} - C.{x|x≠
 ,x∈R,k∈Z}
,x∈R,k∈Z} - D.{x|x≠
 +kπ,x∈R,k∈Z}
+kπ,x∈R,k∈Z}
C
分析:利用正切函数y=tanx的定义域为{x|x≠kπ+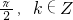 },可以求出y=tan2x的定义域.
},可以求出y=tan2x的定义域.
解答:因为正切函数y=tanx的定义域为{x|x≠kπ+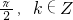 },
},
所以由2x≠kπ+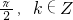 ,得{x|x≠
,得{x|x≠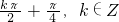 }.
}.
故选C.
点评:本题主要考查了正切函数的定义域的求法,与正切函数有关的定义域可以利用整体代换或者换元法进行求解.
分析:利用正切函数y=tanx的定义域为{x|x≠kπ+
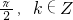 },可以求出y=tan2x的定义域.
},可以求出y=tan2x的定义域.解答:因为正切函数y=tanx的定义域为{x|x≠kπ+
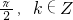 },
},所以由2x≠kπ+
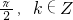 ,得{x|x≠
,得{x|x≠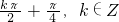 }.
}.故选C.
点评:本题主要考查了正切函数的定义域的求法,与正切函数有关的定义域可以利用整体代换或者换元法进行求解.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目