题目内容
【题目】递增的等差数列![]() 的前
的前![]() 项和为
项和为![]() .若
.若![]() 与
与![]() 是方程
是方程![]() 的两个实数根.
的两个实数根.
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 为多少时,
为多少时,![]() 取最小值,并求其最小值;
取最小值,并求其最小值;
(3)求![]() .
.
【答案】(1)![]() ;(2)所以当
;(2)所以当![]() 或12时,
或12时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;(3)
;(3)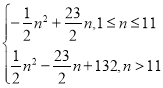
【解析】
(1)先根据韦达定理得两方程,再转化为首项与公差关系,解得结果代入等差数列通项公式;
(2)先根据通项公式确定![]() 变号的项,即可判定
变号的项,即可判定![]() 何时取最小值,再根据等差数列求和公式求最小值;
何时取最小值,再根据等差数列求和公式求最小值;
(3)由(2)知,需分类讨论,根据项的符号去绝对值,再根据去绝对值后与原数列和项关系求结果.
(1)因为![]() 与
与![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,又
,又![]() ,
,
解得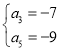 或
或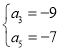 ,又因为该等差数列递增,所以
,又因为该等差数列递增,所以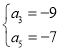 ,
,
则公差![]() ,
,![]() ,
,
所以![]() ;
;
(2)由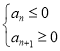 ,即
,即![]() ,解得
,解得![]() ,
,
又![]() ,所以当
,所以当![]() 或12时,
或12时,![]() 取最小值,最小值为
取最小值,最小值为![]() ;
;
(3)由(2)知,当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,
①当![]() 时,
时,
![]()
![]() ;
;
②当![]() 时,
时,
![]()
![]() ,
,
所以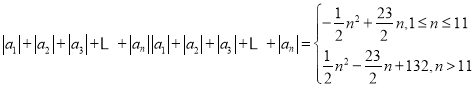 .
.
注:答案还可以为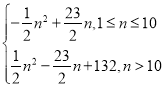 或
或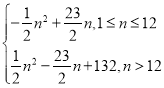 .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目